| Krzysztof Onak | Tomasz Waleń |
| Treść zadania, Opracowanie | Program wzorcowy |
Zwiedzanie miasta
Bajtocka Agencja Turystyczna (w skrócie BAT) chce wejść na rynek
oferując zwiedzanie Bajtogrodu autobusem-kabrioletem.
Należy zbudować siedzibę firmy, w której
będzie się zaczynało i kończyło zwiedzanie.
Trasa zwiedzania musi przechodzić wszystkimi ulicami miasta,
w przeciwnym przypadku turyści mogliby podejrzewać, że nie zobaczyli
czegoś bardzo interesującego.
Ulice nie muszą być proste i mogą przebiegać tunelami lub wiaduktami.
Wszystkie ulice są dwukierunkowe.
Każda ulica łączy dwa skrzyżowania.
Z każdego skrzyżowania w czterech kierunkach wychodzą ulice.
Może się zdarzyć, że dwa skrzyżowania są połączone więcej niż jedną ulicą.
Na ulicach nie wolno zawracać, ale można to robić na skrzyżowaniach.
Ponadto wiadomo, że z każdego skrzyżowania da się dojechać do każdego innego.
Przy każdej ulicy, dokładnie w połowie drogi pomiędzy
skrzyżowaniami, które łączy ulica, znajduje się szczególnie godna
podziwu atrakcja turystyczna
(np. piękny widok, pomnik lub inny zabytek),
wywierająca na zwiedzających "`wrażenie'' określone nieujemną
liczbą całkowitą.
Siedziba BATu powinna znajdować się przy jednej z takich atrakcji.
Przy doborze trasy zwiedzania należy brać pod uwagę zainteresowanie
turystów, które może się zmieniać w trakcie zwiedzania.
Przejechanie autobusem jednej bajtomili powoduje
spadek zainteresowania o jeden.
Przejechanie po raz pierwszy obok danej atrakcji
turystycznej zwiększa
zainteresowanie turystów, o liczbę określająca wrażenie, jakie
robi atrakcja.
Początkowo poziom zainteresowania turystów jest równy
wrażeniu, jakie robi atrakcja,
przy której znajduje się siedziba BATu.
Zainteresowanie turystów nie może w trakcie wycieczki nigdy spaść poniżej zera.
Zadanie
Napisz program, który:
- wczyta opis miasta z pliku tekstowego zwi.in,
- znajdzie trasę spełniającą podane wymagania, lub
stwierdzi, że taka trasa nie istnieje,
- zapisze wynik do pliku tekstowego zwi.out.
Wejście
W pierwszym wierszu pliku tekstowego zwi.in znajduje się
jedna liczba całkowita n określająca liczbę skrzyżowań,
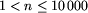 .
Skrzyżowania są ponumerowane od 1 do n, a ulice są
ponumerowane od 1 do 2n.
Kolejnych 2n wierszy opisuje ulice -
(i+1)-szy wiersz w pliku opisuje ulicę o numerze i.
W każdym wierszu znajdują się cztery liczby całkowite
a, b, l, s oddzielone pojedynczymi odstępami.
Liczby a i b to numery skrzyżowań, które łączy
dana ulica,
.
Skrzyżowania są ponumerowane od 1 do n, a ulice są
ponumerowane od 1 do 2n.
Kolejnych 2n wierszy opisuje ulice -
(i+1)-szy wiersz w pliku opisuje ulicę o numerze i.
W każdym wierszu znajdują się cztery liczby całkowite
a, b, l, s oddzielone pojedynczymi odstępami.
Liczby a i b to numery skrzyżowań, które łączy
dana ulica, 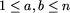 ,
, 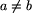 .
Liczba l jest parzystą liczbą całkowitą będącą długością ulicy w
bajtomilach,
.
Liczba l jest parzystą liczbą całkowitą będącą długością ulicy w
bajtomilach, 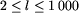 .
Atrakcja turystyczna położona przy danej ulicy robi wrażenie
określone liczbą s,
.
Atrakcja turystyczna położona przy danej ulicy robi wrażenie
określone liczbą s, 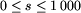 .
.
Wyjście
Pierwszy wiersz pliku tekstowego zwi.out powinien
zawierać jedno słowo TAK, jeżeli istnieje taka trasa,
lub NIE, w przeciwnym przypadku.
Jeśli odpowiedź jest pozytywna to kolejne
wiersze powinny opisywać przykładową trasę.
Drugi wiersz powinien zawierać dokładnie jedną liczbę
całkowitą k równą liczbie skrzyżowań występujących na
trasie zwiedzania.
(Pamiętaj, że ulica, przy której ma znajdować się siedziba BATu łączy
pierwsze i ostatnie skrzyżowanie).
Oznaczmy przez si (dla i = 1, 2, ..., k) numer
ulicy, którą podczas zwiedzania dojeżdża się do i-tego
(w kolejności zwiedzania) skrzyżowania.
Kolejny wiersz powinien zawierać dwie liczby
całkowite s1 i d równe odpowiednio
numerowi ulicy, przy której należy zbudować siedzibę BATu
oraz numerowi pierwszego skrzyżowania, przez które prowadzi trasa
zwiedzania.
Kolejne k-1 wierszy powinno zawierać po jednej liczbie
całkowitej, odpowiednio s2, s3, ..., sk.
Przykład
Dla pliku wejściowego zwi.in
4
1 2 4 6
2 4 2 4
3 2 4 2
4 3 10 8
2 1 8 7
4 3 2 1
1 4 2 6
3 1 4 5
poprawną odpowiedzią jest plik wyjściowy zwi.out
TAK
8
5 2
2
6
3
1
8
4
7
Rozwiązanie
W grafie nieskierowanym definiujemy cykl Eulera jako
cykl przechodzący przez każdą krawędź grafu dokładnie raz.
Rozpatrzmy graf, w którym wierzchołkami będą skrzyżowania,
a krawędziami ulice. Nietrudno dostrzec, że istnieje w tym
grafie cykl Eulera, ponieważ każdy wierzchołek ma parzysty
stopień - z każdego skrzyżowania wychodzą
cztery ulice. Znalezienie pewnej trasy przebiegającej
po takim cyklu wydaje się być dobrym pomysłem, gdyż
agencja turystyczna ,,traci'' wówczas najmniej z
zadowolenia turystów. Tymczasem mamy:
Fakt:
W grafie opisanym przez poprawne dane wejściowe istnieje
cykl Eulera.
Weźmy teraz pewien cykl o długości k, gdzie k>2, z
wierzchołkami ponumerowanymi kolejno od 1 do k. Przypiszmy
każdemu wierzchołkowi pewną nieujemną liczbę - wierzchołkowi
nr i przyporządkowujemy liczbę wi. Niech li będzie
długością krawędzi od wierzchołka nr i do i+1, jeśli
i<k, albo do 1 w przeciwnym przypadku. Rozważamy teraz
następującą sytuację: wybieramy pewien wierzchołek i
obchodzimy cykl w kierunku zgodnym z numeracją
 , wracając do punktu wyjściowego.
Przypuśćmy, że przejście krawędzi kosztuje tyle, co
jej długość, a w każdym wierzchołku otrzymujemy
zwrot kosztu wi dla tego wierzchołka.
Niech
, wracając do punktu wyjściowego.
Przypuśćmy, że przejście krawędzi kosztuje tyle, co
jej długość, a w każdym wierzchołku otrzymujemy
zwrot kosztu wi dla tego wierzchołka.
Niech 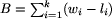 i przyjmijmy, że na początku dysponujemy kapitałem
równym 0. Wówczas prawdziwe jest następujące stwierdzenie:
i przyjmijmy, że na początku dysponujemy kapitałem
równym 0. Wówczas prawdziwe jest następujące stwierdzenie:
Fakt:
Cykl można obejść zachowując zawsze nieujemne konto wtedy
i tylko wtedy, gdy 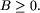
Dowód: Przypuśćmy najpierw, że cykl można
obejść w ten sposób. Wtedy bilans podróży wyrażający się
jako B musi być nieujemny. Teraz dowód
w drugą stronę. Zakładamy, że 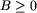 .
Rozpocznijmy symulację w wierzchołku o numerze 1. Przechodzimy
cykl przy założeniu, że możemy mieć ujemny stan konta. Oznaczamy
przez bi stan konta już po dojściu do wierzchołka numer i,
ale jeszcze przed pobraniem wyznaczonej rekompensaty. Na starcie mamy
b1=0. Dla pewnego j otrzymujemy minimalną wartość bj.
Wierzchołek o numerze j będzie naszym nowym wierzchołkiem
startowym. Rozpoczynając drogę tym razem w j dostajemy
nowe wartości b'i takie, że:
.
Rozpocznijmy symulację w wierzchołku o numerze 1. Przechodzimy
cykl przy założeniu, że możemy mieć ujemny stan konta. Oznaczamy
przez bi stan konta już po dojściu do wierzchołka numer i,
ale jeszcze przed pobraniem wyznaczonej rekompensaty. Na starcie mamy
b1=0. Dla pewnego j otrzymujemy minimalną wartość bj.
Wierzchołek o numerze j będzie naszym nowym wierzchołkiem
startowym. Rozpoczynając drogę tym razem w j dostajemy
nowe wartości b'i takie, że:
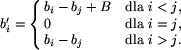
Widać już teraz, że b'i nie może
być ujemne dla żadnego i, gdyż dla każdego i zachodzi
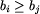 , czyli
, czyli 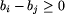 .
.
Wracamy teraz do naszego zadania. Fakt 1 gwarantuje nam istnienie
cyklu Eulera. W dowolnie znalezionym cyklu Eulera
jako wierzchołki traktujemy teraz atrakcje turystyczne.
Fakt 2 daje nam ostatecznie,
że rozwiązanie zadania istnieje wtedy i tylko wtedy, gdy
suma wrażeń dostarczanych przez atrakcje jest nie mniejsza od
sumy długości ulic, a ponadto do znalezienia takiego rozwiązania można posłużyć
się dowolnym cyklem Eulera. Możemy już
zapisać główne kroki algorytmu rozwiązującego zadanie:
- wczytaj dane;
- sprawdź, czy wrażeń dostarczanych przez atrakcje turystyczne
wystarczy na zwiedzenie miasta, a jeśli tak to:
- znajdź cykl Eulera,
- znajdź odpowiedni punkt startowy na skonstruowanym cyklu;
- zapisz wynik.
Punkt 2(a) można zrealizować przechodząc graf w głąb
po nieodwiedzonych jeszcze krawędziach.
Odpowiednia procedura może mieć następujący pseudokod:
| 1 | procedure euler(v); |
| 2 | begin |
| 3 | for w \iinSąsiedzi(v) do |
| 4 | if not odwiedzona[v-w] then |
| 5 | begin |
| 6 | odwiedzona[v-w]:=true; |
| 7 | euler(w); |
| 8 | DopiszKrawędź(v-w); |
| 9 | { dopisuje krawędź na koniec początkowo pustej listy } |
| 10 | end |
| 11 | end |
Podaną procedurę wywołujemy dla dowolnego wierzchołka,
na przykład dla v=1. Nie trudno dowieść, że znajduje ona cykl Eulera.
Przy sprawnym zaimplementowaniu ten krok algorytmu wymaga
czasu O(n).
W implementacji punktu 2(b) algorytmu, można posłużyć
się konstruktywnym dowodem faktu 2. Ta część algorytmu działa
również w czasie O(n). Podsumowując, cały algorytm działa
w czasie O(n).
Testy
Do oceny rozwiązań zawodników użyto kompletu 12 testów:
- zwi1a.in - prosty test poprawnościowy, n=4;
- zwi1b.in - prosty test poprawnościowy na odpowiedź NIE,
n=4;
- zwi2a.in - graf pełny, n=5;
- zwi2b.in - prosty test poprawnościowy, n=10;
- zwi3.in - losowy graf, n=100;
- zwi4.in - okrąg z losowymi wagami, n=1000;
- zwi5.in - dwa nałożone na siebie losowe cykle, n=1000;
- zwi6.in - drabinka, n=3000;
- zwi7.in - dwa nałożone na siebie losowe cykle, n=5000;
- zwi8.in - dwa równoległe okręgi połączone
krawędziami, n=6000;
- zwi9.in - graf losowy, n=10000;
- zwi10.in - dwa nałożone na siebie losowe cykle, n=10000.
Testy zwi1a.in i zwi1b.in oraz zwi2a.in
i zwi2b.in były zgrupowane. Różnice pomiędzy sumą
wrażeń i sumą długości ulic były w testach niewielkie,
a krawędzie w plikach znajdowały się w losowej kolejności.
 , wracając do punktu wyjściowego.
Przypuśćmy, że przejście krawędzi kosztuje tyle, co
jej długość, a w każdym wierzchołku otrzymujemy
zwrot kosztu wi dla tego wierzchołka.
Niech
, wracając do punktu wyjściowego.
Przypuśćmy, że przejście krawędzi kosztuje tyle, co
jej długość, a w każdym wierzchołku otrzymujemy
zwrot kosztu wi dla tego wierzchołka.
Niech 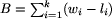 i przyjmijmy, że na początku dysponujemy kapitałem
równym 0. Wówczas prawdziwe jest następujące stwierdzenie:
i przyjmijmy, że na początku dysponujemy kapitałem
równym 0. Wówczas prawdziwe jest następujące stwierdzenie:
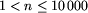 .
Skrzyżowania są ponumerowane od 1 do n, a ulice są
ponumerowane od 1 do 2n.
Kolejnych 2n wierszy opisuje ulice -
(i+1)-szy wiersz w pliku opisuje ulicę o numerze i.
W każdym wierszu znajdują się cztery liczby całkowite
a, b, l, s oddzielone pojedynczymi odstępami.
Liczby a i b to numery skrzyżowań, które łączy
dana ulica,
.
Skrzyżowania są ponumerowane od 1 do n, a ulice są
ponumerowane od 1 do 2n.
Kolejnych 2n wierszy opisuje ulice -
(i+1)-szy wiersz w pliku opisuje ulicę o numerze i.
W każdym wierszu znajdują się cztery liczby całkowite
a, b, l, s oddzielone pojedynczymi odstępami.
Liczby a i b to numery skrzyżowań, które łączy
dana ulica, 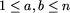 ,
, 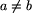 .
Liczba l jest parzystą liczbą całkowitą będącą długością ulicy w
bajtomilach,
.
Liczba l jest parzystą liczbą całkowitą będącą długością ulicy w
bajtomilach, 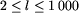 .
Atrakcja turystyczna położona przy danej ulicy robi wrażenie
określone liczbą s,
.
Atrakcja turystyczna położona przy danej ulicy robi wrażenie
określone liczbą s, 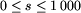 .
.
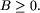
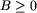 .
Rozpocznijmy symulację w wierzchołku o numerze 1. Przechodzimy
cykl przy założeniu, że możemy mieć ujemny stan konta. Oznaczamy
przez bi stan konta już po dojściu do wierzchołka numer i,
ale jeszcze przed pobraniem wyznaczonej rekompensaty. Na starcie mamy
b1=0. Dla pewnego j otrzymujemy minimalną wartość bj.
Wierzchołek o numerze j będzie naszym nowym wierzchołkiem
startowym. Rozpoczynając drogę tym razem w j dostajemy
nowe wartości b'i takie, że:
.
Rozpocznijmy symulację w wierzchołku o numerze 1. Przechodzimy
cykl przy założeniu, że możemy mieć ujemny stan konta. Oznaczamy
przez bi stan konta już po dojściu do wierzchołka numer i,
ale jeszcze przed pobraniem wyznaczonej rekompensaty. Na starcie mamy
b1=0. Dla pewnego j otrzymujemy minimalną wartość bj.
Wierzchołek o numerze j będzie naszym nowym wierzchołkiem
startowym. Rozpoczynając drogę tym razem w j dostajemy
nowe wartości b'i takie, że:
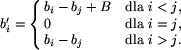
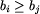 , czyli
, czyli 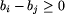 .
.