Omówienie zadania Domino (I etap XXIX OI)

Na początek pokażemy, że jeśli istnieje prostokąt i takie zamalowanie jego pól, żeby istniało dokładnie \(m\) pokryć dominem, to zamalowanie prostokąta o minimalnej szerokości musi spełniać warunek, że każda kolumna nie jest w ogóle zamalowana albo jest zamalowana w całości.

Ponumerujmy kolumny prostokąta rozmiaru \(2\times n\) od lewej do prawej liczbami od 1 do \(n\). Niech \(P[i,j]\) oznacza podprostokąt złożony z kolumn o numerach od \(i\) do \(j\).

Załóżmy nie wprost, że istnieje jakaś kolumna, w której mamy zamalowane dokładnie jedno pole i niech \(i\) będzie najmniejszym numerem takiej kolumny. Wtedy w \(P[1,i-1]\) mamy niezamalowanych parzystą liczbę pól \(2k\), więc te kolumny muszą być pokryte przez dokładnie \(k\) domin. Zatem wolne pole w kolumnie \(i\) musi być pokryte przez poziome domino, którego drugi koniec musi pokrywać pole w kolumnie \(i+1\). Tak więc albo w kolumnie \(i+1\) też mamy jedno zamalowane pole, albo jest ona pusta, ale wtedy to drugie pole musi być pokryte przez poziome domino na kolumnach \(i+1\) oraz \(i+2\).

Niech więc \(j\) będzie drugim numerem kolumny o zamalowanym dokładnie jednym polu (taka kolumna istnieje, bo pokrycie istnieje tylko dla parzystej liczby zamalowanych pól). Wtedy wszystkie kolumny od \(i+1\) do \(j-1\) są niezamalowane a w \(P[i,j]\) jest dokładnie \(2(j-i)\) niezamalowanych pól, które mogą być pokryte \(j-i\) klockami domina na dokładnie jeden sposób.

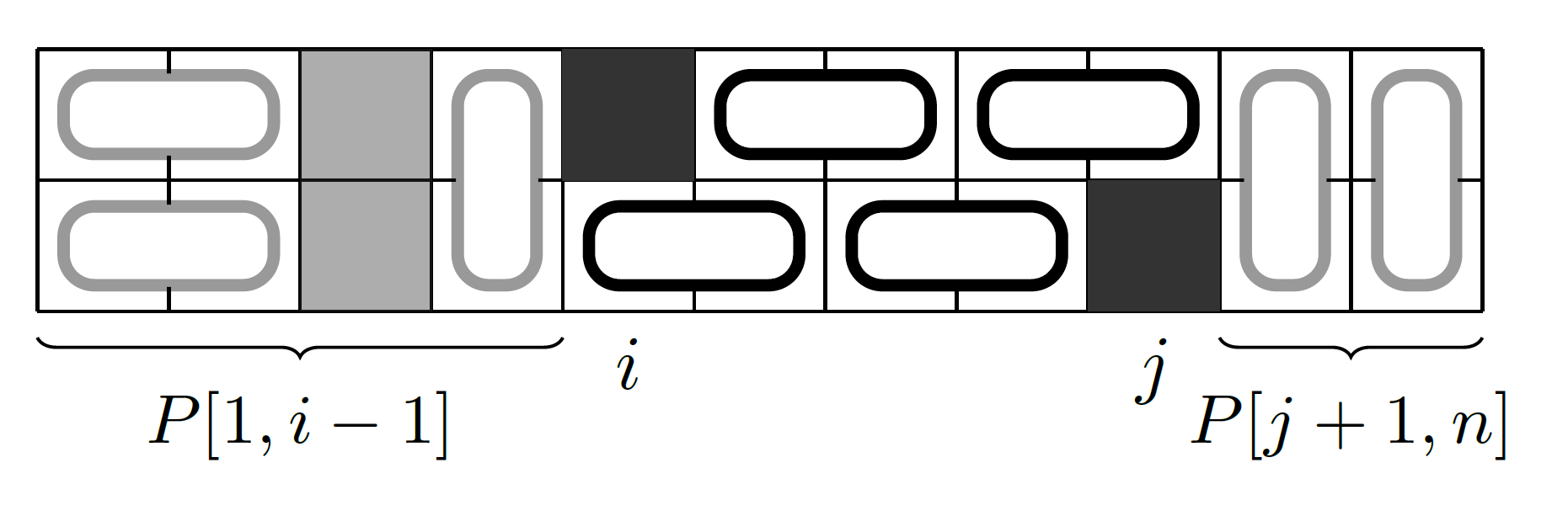
Zatem te jednoznacznie pokryte kolumny rozbijają nam nasz prostokąt na dwa kawałki: \(P[1,i-1]\) oraz \(P[j+1,n]\), które możemy pokryć niezależnie. Nietrudno zauważyć, że jeśli zastąpimy kawałek \(P[i,j]\) przez jedną kolumnę zamalowaną w pełni (a więc też jednoznacznie pokrytą i oddzielającą te dwa kawałki), to dostaniemy prostokąt, który też ma dokładnie \(m\) pokryć, ale jest krótszy o \(j-i\) kolumn, co przeczy minimalności pierwotnego prostokąta. To kończy dowód warunku.

Możemy ten warunek wzmocnić, łatwo pokazując, że ani pierwsza, ani ostatnia kolumna nie mogą być zamalowane (bo można je po prostu odrzucić) oraz żadne dwie kolejne (bo można je zastąpić jedną).

Tak więc, jeśli rozwiązanie istnieje, to składa się z bloków niezamalowanych kolumn, rozdzielonych pojedynczymi kolumnami zamalowanymi w całości.

Podsumowanie

Rozważmy jeden blok niezamalowanych kolumn, czyli prostokąt o wymiarach \(2\times k\). Jest dosyć znanym faktem, że można go pokryć na \(F_k\) sposobów, gdzie \(F\) jest ciągiem liczb Fibonacciego zdefiniowanym następująco: \[F_1 = 1,\quad F_2 = 2,\quad F_k = F_{k-2} + F_{k-1} \textrm{ dla } k \geq 3.\] Ten fakt można łatwo udowodnić przez indukcję. Dla \(k=1\) mamy jedno pokrycie (domino pionowe), co odpowiada \(F_1 = 1\), zaś dla \(k=2\) mamy dwa pokrycia (dwa domina pionowe lub dwa poziome), co odpowiada \(F_2 = 2\).

Dla \(k\geq 3\) patrzymy na pokrycie pierwszej kolumny: jeśli pokrywamy ją dominem pionowym, to pozostałe \(k-1\) kolumn pokryjemy (z założenia indukcyjnego) na \(F_{k-1}\) sposobów. Natomiast jeśli pokrywamy ją dwoma dominami poziomymi (pokrywając również całą drugą kolumnę), to pozostałe \(k-2\) kolumn pokryjemy na \(F_{k-2}\) sposobów. Ostatecznie będziemy mieli \(F_{k-1} + F_{k-2} = F_k\) pokryć, co kończy dowód.

Ponieważ każdy blok pokrywamy niezależnie, liczba pokryć całego prostokąta jest iloczynem liczby pokryć bloków. Zatem rozwiązanie istnieje wtedy, gdy \(m\) jest iloczynem pewnych liczb Fibonacciego.

Jeśli więc mamy rozkład \(m = F_{k_1} \cdot F_{k_2} \cdot \ldots \cdot F_{k_s}\), to możliwym rozwiązaniem jest prostokąt o szerokości \(n = k_1 + k_2 + \ldots + k_s + s-1\) i zamalowanych odpowiednich \(s-1\) kolumnach. Zatem szukamy takiego ciągu \(k_1, k_2, \ldots, k_s\), który minimalizuje tę sumę.

Rekurencyjne generowanie rozkładów

Możemy rekurencyjnie wygenerować wszystkie ciągi, których iloczyny nie przekraczają \(m\). W poniższej procedurze argument \(\texttt{iloczyn}\) oznacza iloczyn konstruowanego ciągu, \(\texttt{pos}\) jest pozycją liczby Fibonacciego, którą aktualnie rozważamy do domnożenia, a \(\texttt{s}\) jest szerokością konstruowanego prostokąta. Zakładamy, że mamy wygenerowaną tablicę liczb Fibonacciego \(\texttt{f}\).

    ans = defaultdict(lambda: 10**9)

    def rek(iloczyn, pos, s):
        ans[iloczyn] = min(ans[iloczyn], s)
        if f[pos] <= m // iloczyn:
            rek(iloczyn * f[pos], pos, s + 1 + pos)
        if pos+1 < len(f):
            rek(iloczyn, pos+1, s)

    rek(1, 2, -1)
    return ans[m]

Co prawda jest to rozwiązanie wykładnicze, ale można sprawdzić eksperymentalnie, że dla \(m=10^9\) w krótkim czasie znajdzie odpowiedź (więc również będzie działać dobrze dla mniejszych liczb, gdyż tak naprawdę generuje wszystkie odpowiedzi dla liczb nie większych niż \(m\)). Zatem przejdzie ono drugie podzadanie. Niestety, dla \(m=10^{18}\) jest zbyt wolne.

Rozkłady dla danego \(m\)

Możemy jednak wykorzystać fakt, że potrzebujemy znać odpowiedź dla tylko jednej wartości \(m\) i generować tylko takie ciągi, których iloczyny dają się rozszerzyć do \(m\), zatem tylko te, które dzielą \(m\):

    ans = 10**9

    def rek(zostalo, pos, s):
        if zostalo == 1:
            ans = min(ans, s)
        else:
            if zostalo % f[pos] == 0:
                rek(zostalo // f[pos], pos, s + 1 + pos)
            if pos+1 < len(f):
                rek(zostalo, pos+1, s)

    rek(m, 2, -1)
    return ans

Ponieważ funkcja "liczba dzielników" nie rośnie zbyt szybko (największa możliwa liczba dzielników dla liczb nie większych niż \(10^{18}\) wynosi \(103\,680\) i występuje dla \(897\,612\,484\,786\,617\,600\)), a liczb Fibonacciego nie większych niż \(10^{18}\) jest 86, więc liczba przejrzanych par (\(\texttt{zostalo}, \texttt{pos}\)) przez ten algorytm to około 9 milionów. Jeśli zatem przerobić go tak, aby dla danej pary znajdował minimalną odpowiedź \(\texttt{s}\) oraz dodać spamiętywanie (np. przy pomocy tablicy haszującej), to możemy mieć pewność, że zmieści się w czasie dla każdego \(m \leq 10^{18}\).

Okazuje się jednak, że te zmiany nie są konieczne i nawet taki niezoptymalizowany program zaliczy wszystkie podzadania. Wynika to z faktu, że liczby Fibonacciego w rozkładzie na czynniki pierwsze mają w większości przypadków co najmniej po jednym unikalnym czynniku pierwszym (czyli takim, którego nie mają inne liczby), a w takich przypadkach obecność (lub nieobecność) takiego czynnika w \(m\) jednoznacznie determinuje, czy tę liczbę Fibonacciego dostaniemy w odpowiedzi.