Omówienie zadania Druk (I etap XXIX OI)

Ponieważ w zadaniu mamy wypisać wszystkie możliwe długości szablonu, którymi można wydrukować tabliczkę, więc możemy spróbować dwuczęściowego rozwiązania:

• Najpierw wygenerujemy pewien zbiór słów, będących kandydatami na szablon. Nie każde z tych słów musi być szablonem, ale chcemy, aby każdy prawidłowy szablon był w tym zbiorze oraz żeby zbiór ten był możliwie mały.
• Następnie dla każdego słowa ze zbioru niezależnie sprawdzimy, czy rzeczywiście jest ono prawidłowym szablonem.

Na koniec wypiszemy długości znalezionych szablonów. Oczywiście złożoność czasowa rozwiązania będzie zależeć od liczby słów w zbiorze kandydatów oraz szybkości działania procedury sprawdzającej.\

Generowanie zbioru kandydatów

Na początek zastanówmy się, jak wygląda pasek pokrywający górne lewe pole tabliczki. Musi być on zaczynać się w tym polu i być albo poziomy, albo pionowy. Mamy zatem dokładnie \(m\) kandydatów poziomych na szablon (będących prefiksami górnego wiersza tabliczki) oraz \(n\) kandydatów pionowych (będących prefiksami lewej kolumny). Daje nam to razem \(n+m-1\) kandydatów.

Możemy jednak zrobić jeszcze jedną, dość oczywistą obserwację. Na tabliczce mamy \(n\cdot m\) liter, a każda litera musi być wydrukowana dokładnie raz przez jedno przyłożenie szablonu. Zatem, jeśli szablon ma długość \(s\), to musimy go przyłożyć do tabliczki dokładnie \(nm/s\) razy, zatem \(s\) musi być dzielnikiem \(nm\). Zatem możemy ze zbioru kandydatów wyrzucić wszystkie słowa, których długości nie dzielą \(nm\).

Można jednak pójść dalej z pomysłem na dzielniki i zrobić ciut mniej oczywistą obserwację, która również będzie wynikać z tego, kiedy paskami o wielkości \(s \times 1\) (lub \(1 \times s\)) jesteśmy w stanie pokryć prostokąt rozmiaru \(n \times m\).

W każde pole tabliczki wpiszmy jedną z \(s\) liczb ze zbioru \(S = \{0,1,2,\ldots,s-1\}\). Liczbą w \(i\)-tym wierszu i \(j\)-tej kolumnie (przy czym wiersze i kolumny numerujemy od 0) tabliczki będzie \((i+j) \bmod s\):

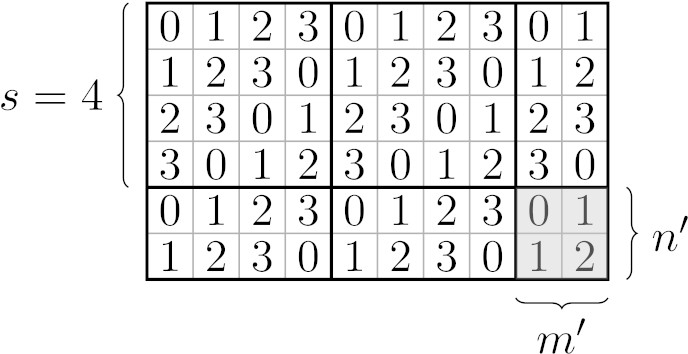
Na takiej tabliczce każde przyłożenie paska długości \(s\) (pionowe lub poziome) będzie pokrywało wszystkie \(s\) liczb ze zbioru \(S\). Tak więc, jeśli tabliczkę da się pokryć szablonem, to każda z liczb musi wystąpić w niej tyle samo razy – dokładnie \(nm/s\).

Załóżmy więc nie wprost, że \(s\) dzieli \(nm\), ale nie dzieli ani \(n\) ani \(m\). Dopóki \(n > s\), to usuwamy z prostokąta \(s\) górnych wierszy. Usunięte fragmenty da się pokryć paskami rozmiaru \(s \times 1\) i zawierają one wszystkie liczby z \(S\) – każdą po \(m\) razy. Analogicznie, dopóki \(m > s\), to usuwamy z prostokąta \(s\) lewych kolumn (takie fragmenty da się pokryć paskami rozmiaru \(1 \times s\)).

Na końcu zostanie nam prostokącik spełniający \(n' < s\), \(m' < s\) oraz \(n'm'\) dzieli \(s\). Tak więc \(n'm' = sx\) dla pewnego \(x < r = \min(n',m')\). Warunkiem koniecznym (choć niekoniecznie wystarczającym) istnienia pokrycia jest to, żeby każda liczba ze zbioru \(S\) występowała w tym prostokąciku \(x\) razy. Ale nietrudno się przekonać, że liczba \(r-1\) będzie występowała co najmniej \(r > x\) razy. Mamy więc sprzeczność, co kończy dowód, że \(s\) musi dzielić \(n\) lub \(m\).

Niech \(d\) będzie liczbą dzielników liczb \(n\) i \(m\) (z powtórzeniami). Mamy wtedy do rozważenia \(d\) kandydatów. Zważywszy na to, że \(n, m \leq 1000\), to największa liczba dzielników dla pojedynczej liczby wyniesie tylko 32 (dla liczby 840), tak więc będziemy musieli rozważyć co najwyżej \(d \leq 64\) kandydatów.

Przypadek tabliczki unarnej

Zanim przejdziemy do ogólnej procedury sprawdzania kandydata, zatrzymajmy się na moment nad przypadkiem szczególnym, gdy cała tabliczka zawiera tylko jedną literę. Wtedy wszyscy kandydaci też będą unarni i wystarczy po prostu sprawdzić, czy paski długości \(s\) są w stanie pokryć prostokąt. Ale łatwo pokazać, że jest to możliwe dla każdego kandydata: jeśli \(s\) dzieli \(n\), to pokrywamy prostokąt samymi pionowymi paskami, a jeśli \(s\) dzieli \(m\) to samymi poziomymi.

Zatem jako odpowiedź wypisujemy wszystkie dzielniki liczb \(n\) i \(m\).

Sprawdzanie jednego kandydata

Teraz zakładamy, że tabliczka zawiera przynajmniej dwie różne litery. Mając ustalone słowo o długości \(s\) mamy sprawdzić, czy jest ono szablonem pokrywającym tabliczkę. Jeśli to słowo jest unarne, to możemy od razu zwrócić odpowiedź negatywną – na pewno nie pokryje tabliczki. Zakładamy zatem, że również w słowie \(s\) występują co najmniej dwie różne litery. (Tak naprawdę muszą w nim występować wszystkie litery, które występują na tabliczce, i dokładnie w tych samych proporcjach. Zaimplementowanie tego sprawdzenia pozwala szybko odsiewać dużą część kandydatów.)

Spróbujemy skonstruować pokrycie, przeglądając pola tabliczki wierszami od góry do dołu, a w każdym wierszu od lewej do prawej. Będziemy utrzymywać niezmiennik, że wszystkie przejrzane pola są już pokryte. Gdy aktualnie przeglądane pole jest już pokryte, pomijamy je. Jeśli nie jest pokryte, to musimy je pokryć paskiem, który zaczyna się w tym polu, przy czym należy podjąć decyzję, czy będzie to poziomy czy pionowy pasek. W czasie \(O(s)\) możemy sprawdzić oba przyłożenia i jeśli żadne nie jest prawidłowe, to kończymy sprawdzenie z wynikiem negatywnym, a jeśli tylko jedno z nich jest prawidłowe, to zaznaczamy pokryte pola i kontynuujemy.

W końcu jeśli oba przyłożenia są prawidłowe, to musimy albo sprawdzić obie możliwości, albo na podstawie jakiegoś kryterium wybrać którąś z nich. W pierwszym przypadku uzyskamy rozwiązanie potencjalnie wykładnicze, co nie będzie nas satysfakcjonowało. Okazuje się jednak, że istnieje bardzo proste zachłanne kryterium, które tu możemy zastosować: wybieramy zawsze przyłożenie poziome.

Dlaczego to jest poprawne? Oznaczmy przez \(a\) pierwszą literę słowa, przez \(k\) liczbę liter \(a\) na jego początku, a przez \(b\) pierwszą literę różną od \(a\) (czyli literę na pozycji \(k+1\)). Jeśli przyłożenie poziome słowa jest poprawne, to w wierszu mamy \(k\) niepokrytych liter \(a\), za którymi występuje niepokryta litera \(b\). Jeśli zdecydowalibyśmy się pokryć aktualną literę paskiem pionowym, to dla kolejnych \(k\) liter pokrycia poziome byłyby nieprawidłowe, zatem musielibyśmy wykonywać pokrycia pionowe. Ale to nie będzie możliwe dla \(k\)-tej litery, co daje sprzeczność.

Tak więc zachłanna procedura jest poprawna i jeśli rozwiązanie istnieje, to znajdzie je w czasie \(O(nms)\).

Możemy przyspieszyć tę procedurę. Zauważmy, że tak naprawdę to litera \(b\) wymuszała zastosowanie pokrycia poziomego. Możemy więc przeglądnąć każdy wiersz dwa razy. Pierwszy raz będziemy poszukiwać niepokrytych liter \(b\). Dla każdej takiej litery stawiamy poziomy pasek, zaczynając \(k\) liter wcześniej (jeśli się nie da, to kończymy). Następnie jeszcze raz przechodzimy wiersz i teraz muszą pozostać niepokryte jedynie litery \(a\), które pokrywamy paskami pionowymi (znowu, jeśli się nie da, to kończymy).

Taka procedura sprawdzająca zadziała w czasie \(O(nm)\), tak więc cały algorytm będzie miał złożoność czasową \(O(nmd)\).