Omówienie zadania Impreza krasnali (I etap XXIX OI)

Obserwacje

Załóżmy, że \(i\)-ty krasnal miał czapkę o wysokości \(x\). Jego czapka mogła być widziana jedynie przez jego sąsiadów, czyli krasnali o numerach \(i-1\) oraz \(i+1\) (o ile ci istnieją). W związku z tym liczba \(x\) może się pojawić w ciągu wejściowym co najwyżej dwa razy, jako \(h_{i-1} = x\) i/lub \(h_{i+1} = x\).

Z tego wynika, że dowolna liczba \(x\) z przedziału od 1 do \(n\) może się pojawić w ciągu 0, 1 lub 2 razy. Przy czym w tym ostatnim przypadku odległość między jej dwoma wystąpieniami musi być równa dokładnie 2. Jeśli któraś z liczb \(x\) pojawia się więcej niż dwa razy lub jej dwa wystąpienia mają inną odległość – możemy od razu zwrócić 0 jako odpowiedź, bo zeznania krasnali są sprzeczne.

Rozważmy teraz liczby \(x\), które pojawiają się dwa razy. Jeśli mamy \(h_{i-1} = x\) oraz \(h_{i+1} = x\), to wiemy, że \(i\)-ty krasnal musiał mieć czapkę wysokości \(x\). Takiego krasnala nazwiemy \(\textit{pewniakiem}\).

Brak pewniaków

Załóżmy na początek, że nie ma pewniaków, czyli w ciągu każda liczba pojawia się 0 lub 1 razy. (Tak naprawdę skoro ciąg ma długość \(n\), to każda liczba musi pojawić się w nim dokładnie raz, czyli ciąg wejściowy jest permutacją.) Przez \(a\) oznaczymy ciąg możliwych wysokości czapek. Pierwszy krasnal widzi jedynie czapkę drugiego krasnala, więc ta jest wyznaczona jednoznacznie, zatem \(a_2 = h_1\). Z kolei trzeci krasnal widział czapkę drugiego lub czwartego krasnala, ale ponieważ \(h_1 \neq h_3\) (bo ciąg wejściowy nie ma powtórzeń), zatem musiał on opisać czapkę czwartego krasnala, więc \(a_4 = h_3\). W ten sposób przez indukcję możemy pokazać, że dla dowolnego \(i\geq 1\) mamy \(a_{2i} = h_{2i-1}\), czyli czapki krasnali na pozycjach parzystych są wyznaczone jednoznacznie. Podobnie możemy iść od tyłu: ostatni krasnal widzi jedynie czapkę przedostatniego, więc \(a_{n-1} = h_n\). Znowu przez indukcję pokazujemy, że dla dowolnego \(i\geq 1\) mamy \(a_{n-2i+1} = h_{n-2i+2}\). I teraz mamy dwa przypadki w zależności od parzystości \(n\). Dla \(n\) parzystego to przejście ,,od tyłu'' wyznacza nam jednoznacznie jak wyglądają czapki krasnali na pozycjach nieparzystych. To pokazuje, że mamy dokładnie jedną odpowiedź: \(a = h_2 h_1 h_4 h_3 \ldots h_n h_{n-1}\). Z kolei dla \(n\) nieparzystego z przejścia "od przodu" mamy \(a_{n-1} = h_{n-2}\). Z kolei z przejścia ,,od tyłu'' mamy \(a_{n-1} = h_n\), co prowadzi do sprzeczności, bo \(h_{n-2} \neq h_n\). Tak więc w tym przypadku odpowiedzią jest 0.

Istnieją pewniaki

Niech w ciągu jest więc co najmniej jeden pewniak. Ponieważ krasnale siedzący na pozycjach parzystych widzą jedynie czapki krasnali na pozycjach nieparzystych i na odwrót – krasnale z pozycji nieparzystych widzą jedynie czapki z pozycji parzystych, więc możemy rozdzielić nasz ciąg na dwa, w zależności od parzystości pozycji. Zajmijmy się więc wyznaczaniem czapek dla pozycji parzystych – dla pozycji nieparzystych algorytm będzie analogiczny. Załóżmy, że na pozycjach \(2i\) oraz \(2j\) stoją dwaj pewniacy oraz nie ma żadnego innego pewniaka na pozycji parzystej między nimi. Niech \(p = j-i-1\) będzie liczbą tych parzystych pozycji pomiędzy nimi. Zatem \(h_{2i-1} = h_{2i+1}\) oraz \(h_{2j-1} = h_{2j+1}\), a poza tym \(p-1\) liczb \(h_{2k+1}\) dla \(i < k < j-1\) jest różnych. Na pozycjach \(2i+2, \ldots, 2j-2\) mamy \(p\) krasnali. Dokładnie \(p-1\) z nich musi dostać tak czapki, żeby było widoczne tych \(p-1\) liczb, a jeden z nich krasnali dostanie \(\textit{jakąś inną}\) czapkę.

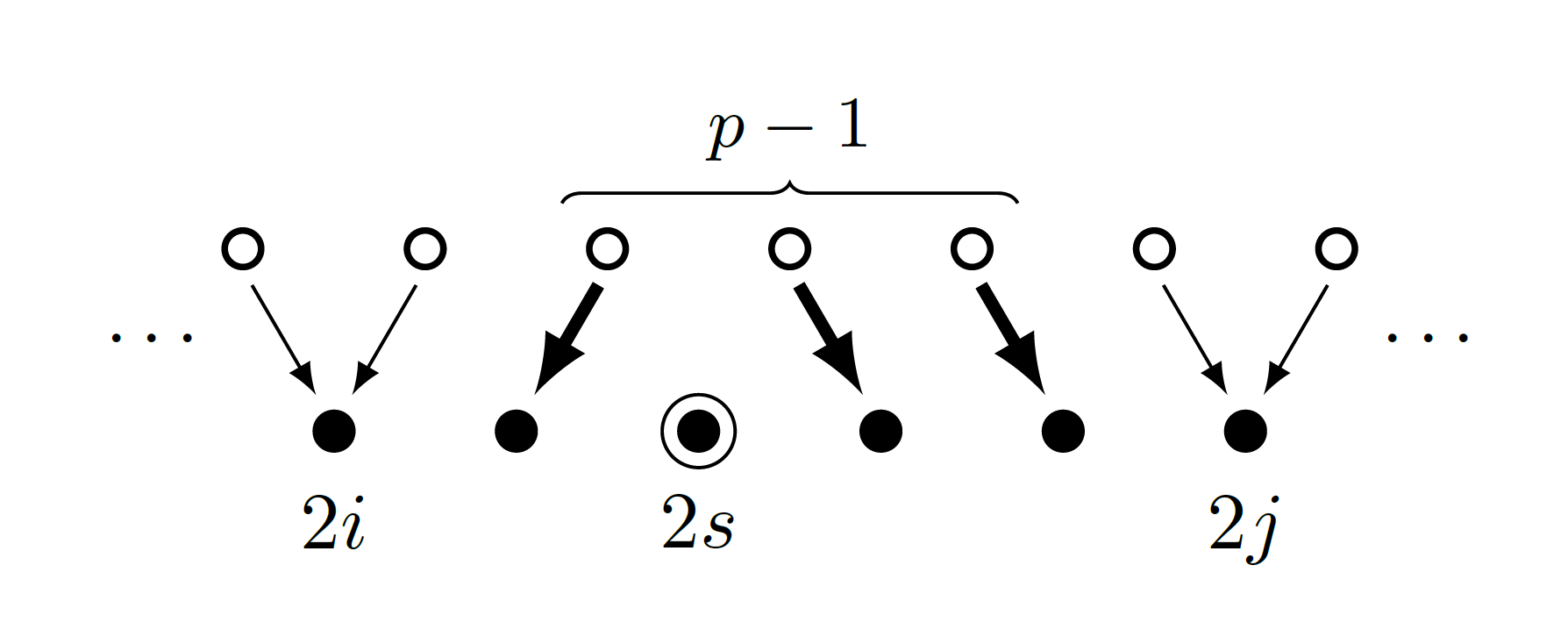
Okazuje się, że dla każdego z \(p\) wyborów, który krasnal będzie miał tę inną czapkę, mamy dokładnie jeden sposób, na który możemy przyporządkować czapki pozostałym krasnalom. A konkretnie, jeśli wybierzemy krasnala \(2s\), to mamy
\[ a_{2k} = \left\{\begin{array}{ll} h_{2k+1} & \textrm{ dla } k < s, \\ h_{2k-1} & \textrm{ dla } k > s. \end{array}\right.\]
Tak więc dla każdego przedziału o długości \(p\) pomiędzy dwoma pewniakami o tej samej parzystości mamy \(p\) możliwości wyboru oraz pozostaje tam jeden krasnal, któremu trzeba będzie przydzielić jedną z czapek, których wysokości nie było w ciągu wejściowym. Podobne rozumowanie możemy zastosować do przedziału przed pierwszym pewniakiem oraz za ostatnim pewniakiem. Dla pierwszego pewniaka parzystego mamy dokładnie jedno przyporządkowanie czapek na lewo od niego. Natomiast dla ostatniego pewniaka parzystego mamy dwie opcje dla czapek na prawo od niego w zależności od parzystości liczby krasnali &ndashl dla nieparzystego \(n\) mamy jedno przyporządkowanie, a dla parzystego \(n\) mamy możliwość wyboru krasnala, który dostanie inną czapkę:

Możemy uniknąć pisania osobnego kodu dla tych przypadków, jeśli rozważymy tylko przedziały pomiędzy pewniakami oraz dla \(n\) parzystego dodamy "wirtualnego" pewniaka na pozycji \(n+2\). Jest jeszcze jedna możliwość do rozważenia, gdy nie ma pewniaków parzystych (ale są jacyś nieparzyści). Wtedy dla \(n\) parzystego mamy dokładnie jedno rozwiązanie, a dla \(n\) nieparzystego mamy sprzeczność.

Podsumowanie

Algorytm na początku sprawdza oczywiste warunki, w których nie istnieje rozwiązanie i wyznacza listę pewniaków parzystych i nieparzystych (dodając ,,wirtualnych''). Następnie przegląda wszystkie pary kolejnych pewniaków o tej samej parzystości i dla każdej z nich mnoży wynik przez liczbę czapek pomiędzy pewniakami. Jeśli w sumie rozważyliśmy \(k\) par, to na końcu mnożymy odpowiedź przez \(k!\), czyli liczbę przyporządkowań \(k\) nieprzyporządkowanych jeszcze czapek dla \(k\) krasnali wybranych w przedziałach.

Złożoność czasowa tego rozwiązania jest \(O(n)\).