Omówienie zadania Układanie kart (I etap XXIX OI)

W zadaniu tym wejściem jest jedna liczba \(n\) (pomijamy w rozważaniach liczbę \(m\), która służy jedynie do ustalenia jak wypisujemy odpowiedź), więc nic nie stoi na przeszkodzie, żeby ręcznie rozpisać sobie pełne rozwiązania dla małych wartości \(n\). Niestety, liczba permutacji, którą musimy przeanalizować (wyrażająca się wzorem \(n!\)) rośnie wykładniczo, więc zadanie to już dla \(n=4\) staje się dość nużące. Możemy jednak zaprząc do niego komputer...

Wizualizacja małych przykładów

Zaczniemy od rozwiązania inżynierskiego – napiszemy program, który dla danego \(n\) przeiteruje się po wszystkich \(n!-1\) permutacjach niekońcowych (czyli z pominięciem "posortowanej" permutacji identycznościowej \(123\ldots n\)). Dla każdej permutacji \(p\) wykona operację Bajtazara: znajdzie kartę do przełożenia i wyznaczy permutację \(q\), która wychodzi po przełożeniu karty. Zapamięta również koszt tej operacji.

Łatwiej będzie nam analizować taki przykład, jeśli przedstawimy go w postaci grafu. Będzie on miał \(n!\) wierzchołków odpowiadających permutacjom, a z każdego wierzchołka (oprócz permutacji identycznościowej) będzie wychodzić dokładnie jedna ważona krawędź (z wierzchołka \(p\) do wierzchołka \(q\) o wadze będącej kosztem operacji). Ten graf będzie więc tak naprawdę drzewem ukorzenionym w wierzchołku permutacji identycznościowej, w którym każda krawędź jest skierowana od dziecka do ojca.

Odpowiedzią do zadania będzie suma wag dla ścieżek z każdego wierzchołka do korzenia.

Do zwizualizowania grafu wykorzystamy program \(\texttt{dot}\) dostępny w dystrybucjach Linuksa. Będzie on potrzebował opisu grafu w następującym formacie (przykład dla \(n=3\)):

    digraph G {
      132 -> 312 [label="1"];
      213 -> 123 [label="1"];
      231 -> 123 [label="2"];
      312 -> 231 [label="2"];
      321 -> 231 [label="1"];
    }

Żeby stworzyć taki opis, napiszemy krótki program \(\texttt{graf.py}\) w języku Python, który wczytuje z wejścia liczbę \(n\) i wypisuje na wyjście opis grafu:

    from itertools import permutations

    n = int(input())

    print('digraph G {')
    for i, p_ in enumerate(permutations(range(n))):
        if i == 0: continue
        p = list(p_)
        card = (p[0] + n-1) % n
        pos = p.index(card)
        q = [card] + p[:pos] + p[pos+1:]
        ps = ''.join([str(x+1) for x in p])
        qs = ''.join([str(x+1) for x in q])
        print('  %s -> %s [label="%d"];' % (ps, qs, pos))
    print('}')

Całość uruchamiamy następującą komendą, która generuje plik \(\texttt{graf.pdf}\) z obrazkiem grafu:

    echo 3 | python graf.py | dot -Tpdf -Grankdir=BT > graf.pdf

Liczba po komendzie \(\texttt{echo}\) to oczywiście interesująca nas wartość \(n\). Na poniższym rysunku przedstawiono efekty tej komendy dla \(n=3\) oraz \(n=4\):

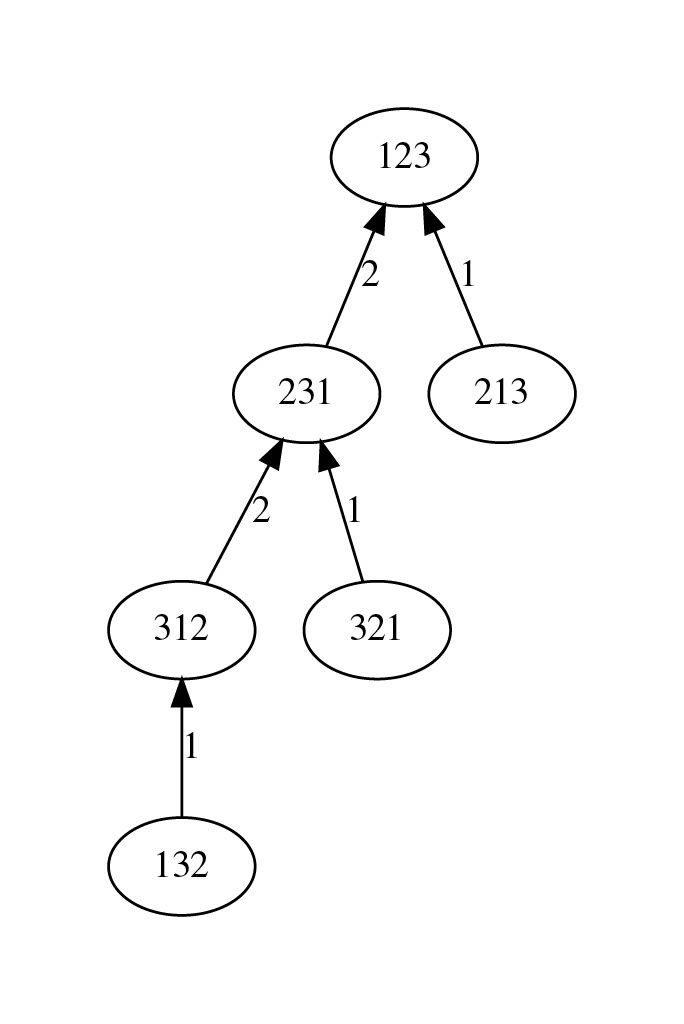
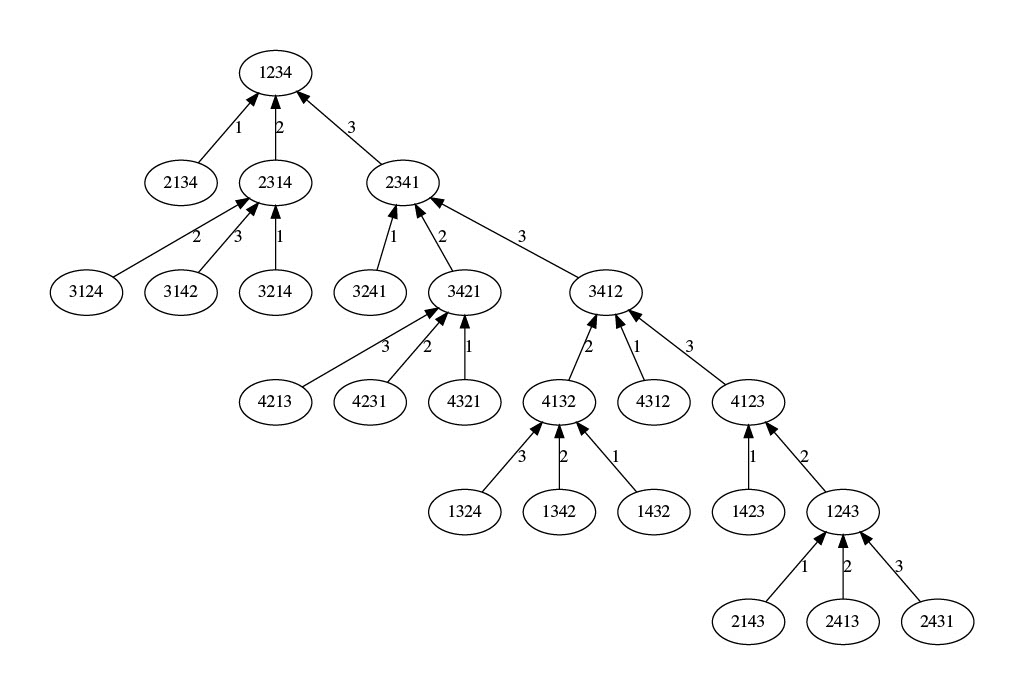
Analiza drzewa

Dzięki takiej wizualizacji możemy dostrzec pewne regularności w drzewie, tym bardziej widoczne dla \(n=5\) lub \(n=6\). Składa się ono z "głównej" ścieżki długości \(n\), która \(n-1\) krawędziami o wadze \(n-1\) łączy kolejne rotacje cykliczne permutacji identycznościowej (w każdej takiej permutacji operacja Bajtazara przekłada ostatnią kartę). Do każdego z wierzchołków ścieżki dochodzą też krawędzie o wagach \(1, 2, \ldots, n-2\), które dołączają do niej pewne poddrzewa. Krawędzią o wadze 1 jest dołączane zawsze poddrzewo jednowierzchołkowe. Krawędzią o wadze 2 jest dołączane drzewo o dwóch poziomach, jego korzeń ma krawędzie o wszystkich wagach \(1,2,\ldots,n-1\).

Dalsza analiza drzew pozwala nam na wysnucie przypuszczenia, że wszystkie drzewa dołączane krawędziami o wadze \(i\) (dla \(1\leq i \leq n-2\)) mają co prawda różne permutacje w wierzchołkach, ale kształtem i wagami są izomorficzne; oznaczmy je przez \(T_i\) (w szczególności \(T_1\) jest drzewem jednowierzchołkowym). Drzewo \(T_i\) ma \(i\) poziomów, a każdy wierzchołek jest albo liściem, albo ma \(n-1\) krawędzi do synów.
Jeszcze dalsza analiza utwierdza nas w przekonaniu, że drzewa \(T_i\) powstają rekurencyjnie. Jak mówiliśmy, drzewo \(T_1\) jest pojedynczym wierzchołkiem. Natomiast drzewo \(T_k\) dla \(k\geq 2\) jest wierzchołkiem do którego dochodzą krawędzie o wagach \(w = 1, 2, \ldots, n-1\), każda podczepiająca drzewo \(T_{\min(w, k-1)}\).

Można więc łatwo napisać rekurencję, która wyznaczy liczbę wierzchołków \(W[k]\) w drzewie \(T_k\) (czyli korzeń plus liczba wierzchołków wszystkich poddrzew):
\[W[k] = 1 + \sum_{1 \leq w \leq n-1} W[\min(w, k-1)]\]
Zapisanie analogicznego wzoru dla tablicy \(S\) pozostawiamy jako ćwiczenie dla Czytelnika.

Dowód poprawności

Dla pełności rozwiązania należałoby formalnie udowodnić, że każde drzewo permutacji ma rzeczywiście taki kształt, jak opisaliśmy powyżej. Niech \(p\) będzie pewną permutacją kart. Kluczowa tutaj będzie długość \(k\) "arytmetycznego prefiksu" tej permutacji, w którym każda kolejna liczba jest większa o 1 od poprzedniej (przy czym po \(n\) może następować 1). Długość tego prefiksu nazwiemy \(\textit{rangą}\) permutacji. W szczególności rotacje cykliczne permutacji identycznościowej (czyli \(n\) permutacji z głównej ścieżki drzewa) to jedyne permutacje o randze \(n\).

Zauważmy, że każda operacja na permutacji o randze mniejszej niż \(n\) zwiększa jej rangę. Zwiększenie jest o 1 lub więcej, bo "prefiks arytmetyczny" jest rozszerzany z lewej o przekładaną kartę i może być rozszerzony z prawej o liczby występujące w oryginalnej permutacji za przekładaną kartą:

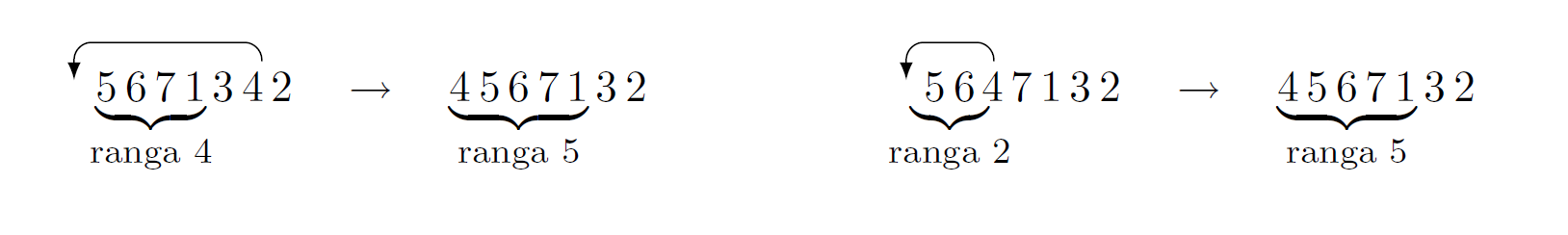
Co łączy rangi permutacji z drzewem? Otóż w korzeniu drzewa \(T_k\) znajduje się zawsze permutacja o randze \(k\).
Dowiedziemy tego, pokazując jak wyglądają dzieci danej permutacji \(p\), czyli z jakich permutacji \(q\) przy pomocy jednej operacji możemy uzyskać permutację \(p\). Jeśli \(p\) ma rangę 1, to nie ma żadnych dzieci, bo muszą one mieć rangę niższą.

Jeśli zaś \(p\) ma rangę \(k>1\) i zaczyna się liczbą \(x\), to permutacja \(q\) wygląda tak, że przesuwamy liczbę \(x\) o pewną liczbę pozycji w prawo (od 1 do \(n-1\)). Jeśli przesunęliśmy ją o co najmniej \(k-1\) pozycji, to permutacja \(q\) ma rangę \(k-1\), jeśli zaś o \(w < k-1\) pozycji, to liczba \(x\) wypadnie w środku prefiksu, zmniejszając rangę permutacji do \(w\). Przesunięcie jest oczywiście kosztem operacji, więc widać, że permutacja o randze \(k\) jest połączona krawędziami \(w=1,\ldots,n-1\) z permutacjami o rangach \(\min(w,k-1)\).

Przypadkiem szczególnym są permutacje cykliczne (czyli o randze \(n\)), w których przesunięcie o \(n-1\) prowadzi z powrotem do permutacji cyklicznej.

Na koniec warto zauważyć, że do przeprowadzenia powyższego dowodu (i w konsekwencji rozwiązania zadania) nie było konieczne wykonanie wizualizacji małych przykładów. Zamiast tego można było popatrzeć na zachowanie operacji Bajtazara dla różnych permutacji i odkryć, że kluczową rolę w klasyfikacji permutacji odgrywa tu długość ich "arytmetycznych prefiksów". Jednak im więcej mamy intuicji związanych z zadaniem (a wizualizacje takich intuicji dostarczają), tym łatwiej nam takich odkryć dokonywać.