


| History of OI -> XIII OI 2005/2006 -> Problems |  |

Task: The Disks
Memory limit: 32MB
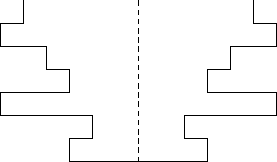
For his birthday present little Johnny has recieved from his parents a new plaything which consists of a tube and a set of disks. The aforementioned tube is of unusual shape. Namely, it is made of a certain number of cylinders (of equal height) with apertures of different diameters carved coaxially through them. The tube is closed at the bottom, open at the top. An exemplary tube consisting of cylinders whose apertures have the diameters: 5cm, 6cm, 4cm, 3cm, 6cm, 2cm and 3cm is presented in the image bellow.
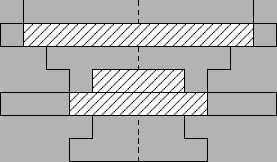
Johnny has invented a following game: having a certain set of disks at his disposal, he seeks to find what depth the last of them would stop at, assuming that they are being thrown into the centre of the tube. If, for instance, we were to throw disks of consecutive diamaters: 3cm, 2cm and 5cm, we would obtain the following situation:
The game being difficult, Johnny constantly asks his parents for help. As Johnny's parents do not like such intelectual games, they have asked you - an acquaintance of theirs and a programmer - to write a programme which will provide them with answers to Johnny's questions.
Task
Write a programme which:- reads the description of the tube and the disks which Johnny will throw into it from the standard input,
- computes the depth which the last disk thrown by Johnny stops at,
- writes the outcome to the standard output.
Input
The first line of the standard input contains two integers n and m ( 1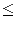 n, m
n, m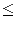 300 000) separated by a single space
and denoting the height of Johnny's tube (the number of cylinders it comprises) and the number of disks Johnny intends to throw into it, respectively.
The second line of the standard input contains n
integers
r1, r2,...,rn
(
1
300 000) separated by a single space
and denoting the height of Johnny's tube (the number of cylinders it comprises) and the number of disks Johnny intends to throw into it, respectively.
The second line of the standard input contains n
integers
r1, r2,...,rn
(
1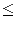 ri
ri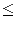 1 000 000 000 for
1
1 000 000 000 for
1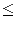 i
i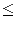 n)
separated by single spaces and denoting the diameters of the apertures carved through the consecutive cylinders (in top-down order), which the tube consists of.
The third line contains m integers
k1, k2,..., km
(
1
n)
separated by single spaces and denoting the diameters of the apertures carved through the consecutive cylinders (in top-down order), which the tube consists of.
The third line contains m integers
k1, k2,..., km
(
1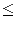 kj
kj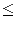 1 000 000 000 for
1
1 000 000 000 for
1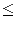 j
j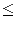 m)
separated by single spaces and denoting the diameters of consecutive disks which Johnny intends to throw into the tube.
m)
separated by single spaces and denoting the diameters of consecutive disks which Johnny intends to throw into the tube.
Output
The first and only line of the standard output should contain a single integer denoting the depth which the last disk stops at. Should the disk not fall into the tube at all, the answer should be 0.
Example
For the input data:7 3 5 6 4 3 6 2 3 3 2 5the correct outcome is:
2

Print friendly version

