History of OI -> XIII OI 2005/2006 -> Problems

News

Links

SIO

MAIN

Task: Frogs

Available memory: 64 MB

A scourge of frogs destroying all the crop has started in Byteotia. A farmer named Byteasar has decided to fight the vermin with peculiar "scarefrogs", that he has set up at certain points of his field. While moving from one place to another, every frog tries to keep as far of them as possible, i.e. maximizes the distance to the closest scarefrog.

The field that belongs to Byteasar has rectangular shape. The frogs leap in directions parallel to the field's sides and their leaps are unitary (of length 1). The scarefrogs-distance, for a given frog's route, is the minimum of all distances from all scarefrogs at all inter-leap-points of the route.

Byteasar already knows the most common starting and destination points of the frogs' routes, therefore he experiments with various deployments of the scarefrogs. He asks you for help, namely he would like you to write a programme that calculates the maximum (over all routes) scarefrogs-distance for a given deployment of scarefrogs -- which we call in short the frogshold distance.

Task

Write a programme that:

reads from the standard input the size of the field, the coordinates of the screfrogs and the source and target position of a frog,
determines the frogshold distance (the maximum scarefrogs-distance a frog may achieve while still being able to reach the target point)
writes the square of this number to the standard output.

Input

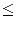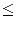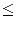The first line of the input contains two integers: w_x and w_y separated by a single space -- the breadth and length of the field ( 2 $$ \leq$% WIDTH=16 HEIGHT=30$ w_x, w_y $$ \leq$% WIDTH=16 HEIGHT=30$ 1 000). 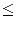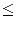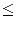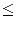The second line of the input contains four integers: p_x, p_y, k_x and k_y separated by single spaces; (p_x, p_y) is the initial position of the frog, (k_x, k_y) is the target (final) position of the frog ( 1 $$ \leq$% WIDTH=16 HEIGHT=30$ p_x, k_x $$ \leq$% WIDTH=16 HEIGHT=30$ w_x, 1 $$ \leq$% WIDTH=16 HEIGHT=30$ p_y, k_y $$ \leq$% WIDTH=16 HEIGHT=30$ w_y). 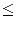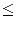The third line of the stanard input contains one integer n -- the number of scarefrogs deployed on the field ( 1 $$ \leq$% WIDTH=16 HEIGHT=30$ n $$ \leq$% WIDTH=16 HEIGHT=30$ w_x^.w_y). The following n lines contain the coordinates of subsequent scarefrogs. The line no. 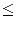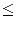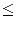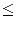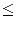i + 3 for 1 $$ \leq$% WIDTH=16 HEIGHT=30$ i $$ \leq$% WIDTH=16 HEIGHT=30$ n contains two integers x_i and y_i separated by a single space -- these are the coordinates of the ith scarefrog ( 1 $$ \leq$% WIDTH=16 HEIGHT=30$ x_i $$ \leq$% WIDTH=16 HEIGHT=30$ w_x, 1 $$ \leq$% WIDTH=16 HEIGHT=30$ y_i $$ \leq$% WIDTH=16 HEIGHT=30$ w_y). No two scarefrogs occupy the same position and none of them is at the point (p_x, p_y) nor (k_x, k_y).

Output

In the first and only line of the standard output one integer should be written, namely the square of the frogshold distance. If the frog cannot avoid leaping directly on some scarefrog the result is 0.

Example

For the following input data:

the correct answer is:

Optimal route of the frog.

Print friendly version