Polish version    English version  
  History of OI -> X OI 2002/2003 -> Problems


 News
 About Olympic
 History of OI
XVII OI 2009/2010
XVI OI 2008/2009
XV OI 2007/2008
XIV OI 2006/2007
XIII OI 2005/2006
XII OI 2004/2005
XI OI 2003/2004
X OI 2002/2003
Schedule
Problems
Stage III - results
Stage II - results
Stage I - results
Stage II
Rules
For contestants
Helpful resources
IX OI 2001/2002
VIII OI 2000/2001
VII OI 1999/2000
VI OI 1998/1999
V OI 1997/1998
IV OI 1996/1997
III OI 1995/1996
II OI 1994/1995
I OI 1993/1994
 OI books
 National team
 Olympic camps
 Photo gallery
 Links
 SIO
 MAIN
X Olympiad in Informatics 2002/2003
Problem: Treasure
Author: Adam Borowski

King Byteasar had hidden a treasure in his castle, and he kept his hiding place in secret. However, whenever he went to war he was afraid he could die and the treasure would get lost. Therefore he chose trustworthy guards and confided partial information needed to find the treasure to each of them. Next he ordered them to go to the underground vaults that lie under the castle and to walk there using the right-hand rule. The vaults were connected by corridors. The corridors did not cross outside the vaults but they could run under other corridors. There were no corridors leading to the same vault they led off. The right-hand rule stated that a guard after entering a vault left it by the next corridor to the right. The guards were appointed different starting positions at entrances to corridors. It might happen that many guards started from the same vault, unless they were entering the same corridor.

The king knew that until he fell or returned from war all guards would loyally follow his orders. However, he was aware that whenever any two or more guards met in some vault they could not resist sharing all the information they knew about the treasure. The guards were not selfish and they shared information even if some of them would not learnt anything new. If some guards started from the same vault they immediately shared the information they initially knew. If they passed one another in corridors, however, they did not talk.

The king pondered if the treasure would still be secure when he safely returned from war. He wanted to know which guards might obtain all the information needed to find the treasure.

Task

Write a program which:
  • reads from the standard input the description of the castle basement, the starting positions of the guards and information each of the guards initially knows,
  • determines the guards who could ever know all the information needed to find the treasure,
  • writes to the standard output the numbers of those guards.

Input

In the first line of the standard input there is one integer n. That is the number of the underground vaults, 2 <= n <= 100. The vaults are numbered from 1 to n. In the following n lines corridors connecting the vaults are described. In the (i + 1)-st line the corridors leading off the i-th vault are described in clockwise order. In each of those lines there are integers separated by single spaces. The first of those numbers, ki, is the number of corridors leading off the i-th vault, 1 <= ki <= n - 1. It is followed, in the same line, by 2ki integers: each leading off corridor is described by two integers. The former is the number of the vault the corridor leads to, and the latter is the length of the corridor: an integer in the range from 1 to 100. The corridors are two-way, i.e. if from a vault a a corridor of length l leads to a vault b then from the vault b a corridor of length l leads to the vault a. Each pair of vaults may be connected by at most one corridor. A guard to walk along a corridor needs exactly the amount of time that is equal to the length of that corridor. We assume the time guards spend in vaults negligible.

In the (n + 2)-nd line there are written two integers k and l, 1 <= k <= 100, 1 <= l <= 100, where k is the number of guards, and l is the number of pieces of information needed to find the treasure. The guards are numbered from 1 to k. The pieces of information concerning the treasure are numbered from 1 to l. The guards are described in the following k lines (the i-th guard is described in the (i + n + 2)-nd line). Each of those lines consists of integers separated by single spaces. The first integer in a line is the number of the vault the corresponding guard starts from. The second number is the number of the vault the guard goes to first. The third number, mi, is the number of pieces of information concerning the treasure the i-th guard initially knows, 0 <= mi <= l. The following mi integers in the line are the numbers of the pieces of information initially known to the i-th guard.

Output

In the first line of the standard output your program should write one integer: the number of guards who could ever know all the information needed to find the treasure. In the following lines there should be written the numbers of those guards in ascending order, one number per line.

Example

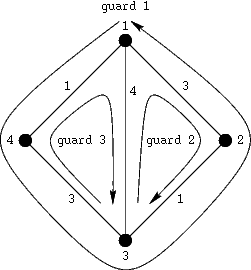
For the following input data: 
4
3 2 3 3 4 4 1
2 1 3 3 1
3 4 3 1 4 2 1
2 1 1 3 3
3 4
1 4 2 2 3
3 1 2 1 2
3 4 2 3 4
the correct answer is in the following output: 
2
2
3

example




Print friendly version