Omówienie zadania Skoczek (III etap XXX OI)

Wstępna obserwacja

Dla uproszczenia wprowadźmy określenie odległości między polami. pole \(A\) jest w odległości \(x\) od pola \(B\), jeśli najmniejsza liczba skoków, w których skoczek jest w stanie przeskoczyć z pola \(A\) do pola \(B\) wynosi \(x\). Zauważmy, że ruchy skoczka są symetryczne - oznacza to, iż jeśli pole \(A\) jest w odległości \(x\) od pola \(B\) to pole \(B\) również jest w odległości \(x\) od pola \(A\).

Wprowadźmy zatem oznaczenie \(\text{odl}(A, B)\) oznaczające odległość pomiędzy polami \(A\) i \(B\).

Dalsza analiza

Na podstawie powyższej obserwacji, możemy utożsamić wynik funkcji \(\texttt{pytanie(x, y)}\) z wartością \(\text{odl}(S, \left(x,y\right))\), gdzie \(S\) oznacza pole, na którym stoi skoczek.

Gdy zapytamy się biblioteczki o wartość \(\text{odl}(S, P_1)\) dla pewnego pola \(P_1\) i otrzymamy odpowiedź \(x_1\), możemy ograniczyć zbiór pól, na których może stać skoczek ze wszystkich pól na planszy do wszystkich pól \(T\) spełniających równość \(\text{odl}(T, P_1) = x_1\).

Jeśli teraz zapytamy się o wartość \(\text{odl}(S, P_2)\) dla pewnego innego pola \(P_2\) i otrzymamy odpowiedź \(x_2\), możemy ograniczyć zbiór potencjalnych pozycji skoczka do pól \(T\) spełniających równości \(\text{odl}(T, P_1) = x_1\) oraz \(\text{odl}(T, P_2) = x_2\).

Później możemy spytać się o wartość \(\text{odl}(T, P_3)\), co pozwoli nam jeszcze bardziej ograniczyć zbiór pól, na których może stać skoczek - i tak dalej, aż na planszy zostanie tylko jedno pole spełniające szereg równości postaci \(\text{odl}(T, P_i) = x_i\).

Pierwszy pomysł

Wprowadźmy oznaczenie pomocnicze \(Z_k\) oznaczające zbiór pól \(T\) spełniających ciąg warunków \(\text{odl}(T, P_1) = x_1\), \(\text{odl}(T, P_2) = x_2\), \(\ldots\), \(\text{odl}(T, P_k) = x_k\).

Wiemy już jaką strategię chcemy zastosować, aby odnaleźć pole, na którym znajduje się skoczek. Pozostają nam do rozwiązania trzy problemy:

1. Jak efektownie znaleźć zbiór pól \(T\) spełniających równość \(\text{odl}(T, P) = x\)?
2. Jak efektownie ograniczyć zbiór \(Z_k\) pól \(T\) spełniających szereg równości \(\text{odl}(T, P_1) = x_1\), \(\text{odl}(T, P_2) = x_2\), \(\ldots\), \(\text{odl}(T, P_k) = x_k\) do zbioru \(Z_{k + 1}\) pól spełniających szereg równości \(\text{odl}(T, P_1) = x_1\), \(\ldots\), \(\text{odl}(T, P_k) = x_k\), \(\text{odl}(T, P_{k + 1}) = x_{k + 1}\)
3. Jak dobrać ciąg pól \(P_1, P_2, \ldots, P_m\) tak, aby ciąg mocy zbiorów \(Z_1, Z_2, \ldots\, Z_m\) był malejący oraz \(\left|Z_m\right| = 1\), niezależnie\(^1\) od ciągu \(x_1, x_2, \ldots\)?

\(^1\) Zależy nam na tym, aby moce zbiorów \(Z\) malały niezależnie od ciągu \(x\), gdyż w treści znajduje się fragment:
Biblioteka nie musi ustalać pozycji skoczka na początku interakcji z Twoim programem. Może ona w trakcie interakcji zmieniać pozycję, o ile nowa pozycja jest nadal zgodna z wynikami zwróconymi przez dotychczasowe wywołania funkcji pytanie.
Oznacza to, iż nasze rozwiązanie musi być odporne na "złośliwość" biblioteczki.

Rozwiążmy te problemy po kolei:

1. Możemy zinterpretować planszę jako graf, którego wierzchołki reprezentują pola planszy, a krawędzi możliwe ruchy skoczka (pola \(A\) i \(B\) są połączone krawędzią, jeśli skoczek jest w stanie przeskoczyć z pola \(A\) do pola \(B\) w jednym ruchu). Przy takiej interpretacji grafowej, jeśli zastosujemy algorytm BFS z początkiem w wierzchołku \(P\), uzyskamy tablicę zawierającą dla każdego pola jego odległość od pola \(P\). Możemy łatwo odczytać z niej zbiór \(T\) spełniających równość \(\text{odl}(T, P) = x\) przechodząc się po wszystkich polach planszy i wybierając te pola, których odległość od pola \(P\) wynosi dokładnie \(x\) - takie rozwiązanie działa w złożoności \(O(n^2)\), co przy ograniczeniu \(n \leq 1000\) jest dla nas zadowalające.
2. Ten problem sprowadza się do efektownego ograniczenia zbioru \(Z_k\) do zbioru \(Z_{k + 1}\). Zauważmy, że \(\displaystyle \forall_{k \in \mathbb{N}}\ Z_{k + 1} \subset Z_k\). Ponadto, przy założeniu, że \(Z_0\) to zbiór wszystkich pól na planszy, rozwiązanie pierwszego problemu pozwala nam przekształcić zbiór \(Z_0\) w zbiór \(Z_1\). Aby przekształcić dowolny zbiór \(Z_k\) w zbiór \(Z_{k + 1}\), wystarczy wybrać do zbioru \(Z_{k + 1}\) wszystkie te elementy ze zbioru \(Z_k\), które spełniają równość \(\text{odl}(T, P_{k+1}) = x_{k+1}\). W ten sposób \(Z_{k + 1}\) otrzymujemy na podstawie \(Z_k\) w złożoności \(O(n^2)\), zatem dowolne \(Z_k\) możemy otrzymać w złożoności \(O(k \cdot n^2)\).
3. Ostatni problem ma najprostsze rozwiązanie - zauważmy, że dla każdego pola tylko ono samo znajduje się w odległości \(0\) od siebie. Wybierając więc ciąg \(P_k\) tak, że \(\displaystyle \forall_{k \in \mathbb{N}}\ P_{k + 1} \in Z_k\) gwarantujemy, iż \(\left|Z_k\right| > \left|Z_{k + 1}\right|\):
   • Jeśli \(\left|Z_k\right| = 1\), to m = k - nie istnieje \(Z_{k + 1}\), ani \(P_{k + 1}\).
   • Wpp. jeśli \(\text{odl}(S, P_k) = 0\), to \(Z_{k + 1} = \{P_k\}\), zatem \(m = k + 1\) oraz \(\left|Z_{k + 1}\right| = 1 < \left|Z_k\right|\).
   • Wpp. jeśli \(\text{odl}(S, P_k) \neq 0\), to \(P_k \not\in Z_{k + 1}\), a więc skoro \(P_k \in Z_k\) oraz \(Z_{k + 1} \subset Z_k\), to \(\left|Z_{k + 1}\right| \leq \left|Z_k\right| - 1\).

Stosując rozwiązanie opisane powyżej, wybierając kolejne elementy ciągu \(P_k\) losowo, otrzymujemy rozwiązanie, które powinno znajdować pozycję skoczka wykonując maksymalnie \(8\) zapytań i otrzymać około \(60\) punktów.

Drobne usprawnienie

Możemy nieco zmodyfikować powyższe rozwiązanie tak, aby mieściło się w \(7\) zapytaniach. Wystarczy, że przed rozpoczęciem wykonywania algorytmu z poprzedniego rozwiązania, ograniczymy \(Z_0\) - zbiór początkowych możliwych pozycji skoczka - kilkoma taktycznymi zapytaniami. Zauważmy, że jeśli zapytamy się o odległość do rogu o współrzędnych \((1,1)\) i otrzymamy odpowiedź \(k\), to znaczy, że pole \(x,y\), na którym znajduje się skoczek musi spełniać nierówności \(x \leq 2k + 1\), \(y \leq 2k + 1\), \(x + y \leq 3k + 1\). Pytając się o pozostałe rogi otrzymamy analogiczne nierówności, zatem po zapytaniu o wszystkie cztery rogi pole, wewnątrz którego znajduje się skoczek będzie bardzo małe. Poniższy rysunek obrazuje jak takie 4 zapytania ograniczają zakres pól, na których może stać skoczek.

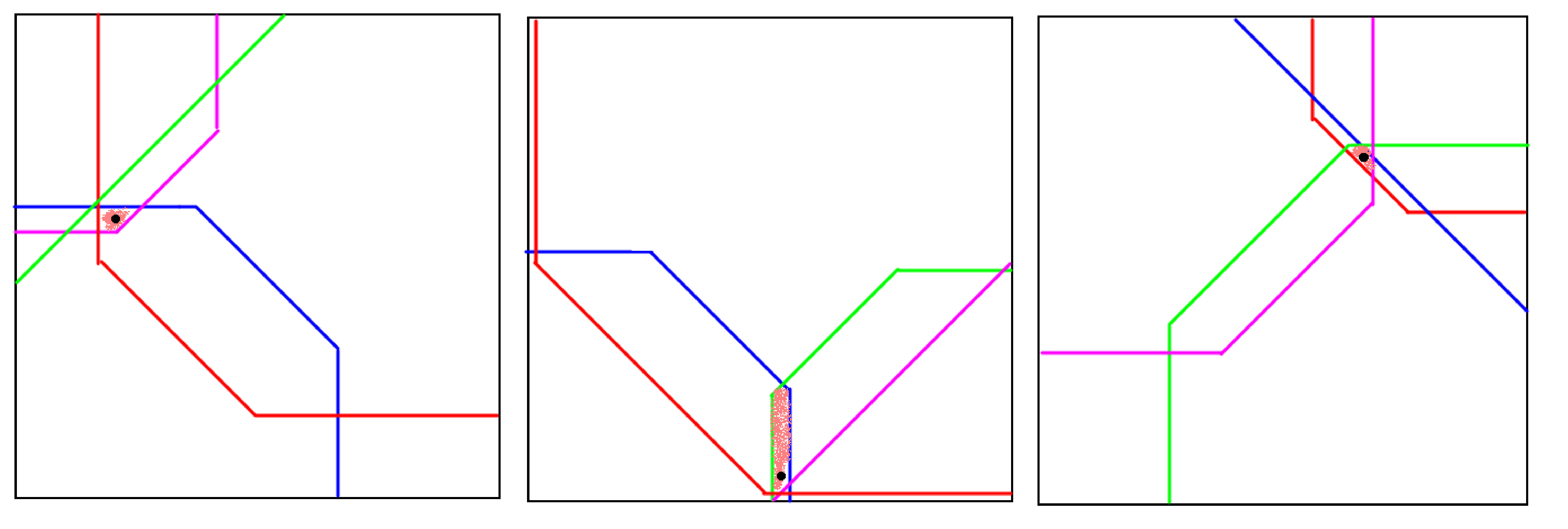
Ponadto, możemy zauważyć, iż możliwe pozycje skoczka muszą leżeć niedaleko łamanych wyznaczonych przez zapytania o rogi - do pól dalekich od łamanej wyznaczonej przez pole \((1,1)\) skoczek doskoczy w mniejszej liczbie skoków, niż \(k\). Możemy więc jeszcze bardziej ograniczyć zakres pól, na których może stać skoczek, jeśli zamiast ograniczyć je do pól spełniających zestaw \(12\) uzyskanych nierówności, postąpimy jak w przejściu ze zbioru \(Z_i\) do \(Z_{i+1}\) - znajdziemy wszystkie pola leżące w odpowiednich odległościach od rogów czterokrotnie przechodząc po planszy algorytmem BFS.

Rozwiązanie, które najpierw pyta o wszystkie 4 rogi, a następnie losuje kolejne zapytania powinno otrzymać podobną liczbę punktów do poprzedniego (zależnie od implementacji, może nawet mniej!), jednak jeśli zaczniemy od zapytań o dowolne 3 rogi, rozwiązanie powinno wykonywać nie więcej niż \(7\) zapytań i otrzymać około \(75\) punktów.

Rozwiązanie wzorcowe

Jeśli chcemy otrzymać \(100\) punktów za zadanie musimy zmieścić się w \(6\) zapytaniach. Niestety w tym celu należy zmienić podejście doboru pól, o odległość do których się pytamy. Pierwsze trzy pola, o które będziemy chcieli zapytać to wciąż będą rogi planszy. Teraz z pozostałych pól, na których może stać skoczek musimy w \(3\) zapytaniach wyłonić odpowiedź. W tym celu zastosujemy algorytm minimax.

Oznaczmy \(Z\) jako zbiór pól, na których może stać skoczek po wykonaniu zapytań o wybrane 3 rogi. Niech \(Z(A, k) = \{P \in Z : \text{odl}(P, A) = k\}\) to podzbiór pól z \(Z\) leżących w odległości \(k\) do pola \(A\). Niech pole, na którym znajduje się skoczek nazywa się \(S\).

Pierwsze z pozostałych \(3\) zapytań będziemy chcieli wybrać tak, aby dla każdej możliwej odpowiedzi biblioteczki dało się znaleźć skoczka w co najwyżej \(2\) kolejnych zapytaniach. Oznacza to, że aby zapytanie o pole \(A\) pozwalało nam na znalezienie wyniku w \(3\) zapytaniach, dla każdej możliwej wartości \(k = \text{odl}(S, A)\), musimy znaleźć pole \(B_k\), takie, że dla każdej możliwej wartości \(l = \text{odl}(S, B_k)\) jesteśmy w stanie znaleźć pole \(C_{k,l}\) takie, że dla każdej możliwej wartości \(h = \text{odl}(S, C_{k,l})\), \(|Z(A, k)(B_k, l)(C_{k,l},h)| = 1\). Innymi słowy, musi istnieć dokładnie jedno pole w zbiorze \(Z\), które leży w odległości \(k\) od pola \(A\), \(l\) od pola \(B_k\) oraz \(h\) od pola \(C_{k,l}\).

Warto zauważyć, iż zbiór możliwych odległości pola \(S\) od wybranego pola \(A\) to zbiór \(\{\text{odl}(A, P) : P \in Z\}\), gdyż gdyby \(\text{odl(S, A)}\) nie należało do tego zbioru, nie istniało by pole w zbiorze \(Z\), które leży w tej samej odległości od pola \(A\) co pole \(S\).

Rozpatrzenie wszystkich możliwych trójek pól \(A, B, C\) wymagało by złożoności czasowej \(\Omega(n^5)\), zatem musimy wprowadzić pewne ograniczenia na pola, które rozważamy jako warte sprawdzenia. Łatwo zauważyć również, że gdy znajdziemy jedno pole \(A\) umożliwiające zdobycie wyniku w \(3\) zapytaniach nie musimy szukać żadnego innego. Ponadto, wiemy, że wszystkie pola w zbiorze \(Z\) muszą być blisko siebie. Możemy więc, aby zmniejszyć złożoność czasową naszego rozwiązania rozważyć tylko pola w okolicy pól ze zbioru \(Z\), czyli pola ze zbioru \(N(Z, 3)\), gdzie \(N(Z, d) = \{(x,y) \in \mathbb{Z}_+ : \exists_{(x^\prime,y^\prime) \in Z}\ |x - x^\prime| \leq d \text{ oraz } |y - y^\prime| \leq d \}\). Innymi słowy, rozważamy tylko pola odległe od jakiegoś pola z \(Z\) o co najwyżej \(3\) na każdej ze współrzędnych. Jako potencjalne pola \(B_k\) rozważymy tylko pola ze zbioru \(N(Z(A, k), 3)\) i analogicznie dla potencjalnych pól \(C_{k,l}\). Teraz nasza pesymistyczna złożoność będzie około \(O(|Z|^3 \cdot n^2)\) - mamy \(O(|Z|^3)\) trójek \(A, B, C\) do rozpatrzenia, BFS przeszukuje \(O(n^2)\) pól / ruchów skoczka. BFSa dla danej trójki wywołamy trzykrotnie, a zbiór \(Z\) możemy przechowywać w strukturze \(\texttt{set}\) z STLa, czyli w złożoności \(O(log |Z|) = O(n^2)\)).

Możemy także usprawnić czas, w którym wykonujemy algorytm BFS. Możemy przekazywać funkcji znajdującej odległości od pola \(P\) zbiór pól \(X\), do którego odległości z pola \(P\) nas interesują. I w momencie, gdy BFS odnajdzie odległości do każdego z tych pól, zakończyć jego działanie. Żeby nie potrzebować czyścić tablicy odległości, z której korzysta algorytm BFS, możemy użyć leniwych tablic. Tak usprawniony BFS powinien potrafić odnaleźć interesujące nas odległości w złożoności czasowej około \(O(|Z| \cdot D)\), gdzie \(D = \max\{odl(P_1,P_2) : P_1, P_2 \in N(Z, 3)\}\). Teraz nasza całościowa złożoność powinna być rzędu \(O(|Z|^4 \cdot D)\).

Aby nasze rozwiązanie zmieściło się w limitach czasowych jest jednak kluczowa jeszcze jedna optymalizacja: po obliczeniu w ilu zapytaniach potrafimy znaleźć skoczka w danym podzbiorze \(Z\), musimy zapamiętać ten wynik, by nie liczyć go ponownie. Do tego celu warto użyć struktury \(\texttt{map}\) z STLa.

Reasumując, do implementacji rozwiązania wzorcowego potrzebujemy funkcji rekurencyjnej o następującym przebiegu:

• Funkcja przyjmuje podzbiór pól \(X\), na których może się znajdować skoczek. Wynikiem funkcji jest pole, o który należy zapytać, aby dało się znaleźć odpowiedź w minimalnej liczbie zapytań, niezależnie od odpowiedzi biblioteczki oraz minimalna liczba zapytań, w których jesteśmy w stanie znaleźć skoczka zaczynając od tego zapytania.
• Sprawdzamy w mapie czy policzyliśmy już wynik dla tego zbioru. W mapie trzymamy zarówno pole, o które należy się zapytać biblioteczki, jak i liczbę zapytań, w których otrzymamy wynik. Jeśli wynik policzyliśmy już wcześniej, zwracamy wcześniej policzone pole.
• W przeciwnym przypadku, przechodzimy się po wszystkich polach z okolicy zbioru \(X\), czyli wszystkich pól ze zbioru \(N(Z, 3)\). Dla każdego pola \(P \in N(Z, 3)\):
  • Obliczamy odległość do wszystkich pól z \(X\) od pola \(P\) za pomocą wcześniej opisanego usprawnionego algorytmu BFS. Tworzymy podział zbioru \(X\) na podzbiory pól o równych odległościach od pola \(P\).
  • Dla każdego z tych podzbiorów, który zawiera więcej niż jedno pole, wywołujemy rekurencyjnie naszą funkcję, aby dowiedzieć się w ilu minimalnie zapytaniach potrafimy znaleźć w nim skoczka. Zapisujemy maksymalną z tych wartości, gdyż chcemy zagwarantować, że potrafimy znaleźć odpowiedź niezależnie od odległości skoczka od pola \(P\).
• Wybieramy pole \(P\), dla którego liczba dodatkowych zapytań potrzebnych do znalezienia skoczka była minimalna.
• Teraz liczba zapytań do znalezienia skoczka w zbiorze \(X\) wynosi wynik po zapytaniu o pole \(P\) + 1, a pierwsze pole, o które powinniśmy się zapytać, to pole \(P\). Zapisujemy je w mapie jako wynik dla zbioru \(X\) i zwracamy jako wynik funkcji.

Właściwy kod wyznacza początkowy podzbiór pól \(Z\) pytając się o dowolne trzy rogi planszy i wrzucając do niego wszystkie pola w odległościach od każdego z nich zgodnymi z odpowiedziami biblioteczki. Następnie, dopóki \(|Z|\) > 1, znajdujemy pole, o które chcemy się zapytać za pomocą wywołania naszej funkcji rekurencyjnej na zbiorze \(Z\), pytamy biblioteczkę o odległość skoczka od tego pola i aktualizujemy zbiór \(Z\) usuwając z niego pola niezgodne z wynikiem zapytania. Gdy \(|Z| = 1\), jedyne pole pozostały w tym zbiorze to pole, na którym znajduje się skoczek.

Takie rozwiązanie powinno zawsze znajdować skoczka w co najwyżej \(6\) zapytaniach i mieścić się w limitach czasowych, uzyskując tym samym wynik 100 punktów.