Omówienie zadania Walki robotów (I etap XXXII OI)

Rozwiązanie dla $n \leq 8$

W tym podzadaniu możemy zasymulować wszystkie możliwe gry i sprawdzić, czy w którejś uda nam się wyeliminować wszystkie roboty. Wykorzystamy w tym celu przeszukiwanie z nawrotami (ang. backtracking).

Załóżmy, że podczas symulacji turnieju dochodzimy do stanu, w którym pewna liczba robotów jest już wyeliminowana, a pozostałe dalej biorą udział w grze. Możemy wybrać pewną parę niewyeliminowanych robotów, rozegrać między nimi pojedynek, a następnie odrzucić roboty w nim wyeliminowane. W ten sposób otrzymujemy nowy stan i możemy kontynuować ten proces rekurencyjnie. Oczywiście dla danej sytuacji musimy rozpatrzeć wszystkie możliwe wybory par robotów do pojedynku.

Takie przeszukiwanie rozpoczynamy od stanu, w którym żaden robot nie jest wyeliminowany. Jeśli uda nam się dojść do stanu, w którym wszystkie roboty są wyeliminowane, to kończymy algorytm z odpowiedzią "TAK". W przeciwnym wypadku odpowiadamy "NIE".

Aby efektywnie zaimplementować powyższe rozwiązanie, możemy utrzymywać zbiór niewyeliminowanych robotów w postaci maski bitowej. Nasza symulacja będzie funkcją rekurencyjną przyjmującą maskę bitową jako argument. Wywołanie funkcji będzie polegać na przeiterowaniu się po wszystkich parach różnych zapalonych bitów w masce, rozegraniu pojedynku między odpowiadającymi im robotami i wywołaniu rekurencyjnym z maską bitową odpowiadającą stanowi po wyeliminowaniu robotów z pojedynku.

Złożoność naszego algorytmu możemy oszacować przez $O ((n^{2})^{n - 1})$ , gdyż w każdym kroku mamy $O (n^{2})$ wyborów par robotów do pojedynku oraz wiemy, że w ciągu gry odbędzie się co najwyżej $n - 1$ pojedynków. W praktyce, jak często bywa z przeszukiwaniem z nawrotami, algorytm jest bardzo szybki w porównaniu do swojej asymptotycznej złożoności. Takie rozwiązanie pozwalało więc zaliczyć podzadanie, w którym $n \leq 8$ .

Rozwiązanie dla $n \leq 20$

Powyższe rozwiązanie można przyspieszyć dzięki dokładniejszej analizie naszej funkcji rekurencyjnej. Wystarczy zauważyć, że zachowanie tej funkcji zależy jedynie od przekazanej jej maski bitowej reprezentującej stan gry. Innymi słowy, wywołanie tej funkcji z tą samą maską bitową zawsze da te same rezultaty. Wnioskujemy więc, że nie ma potrzeby wielokrotnego wykonywania funkcji dla tej samej maski. Możemy zatem zapamiętać dla wszystkich możliwych $2^{n}$ masek bitowych, czy nasza funkcja już została dla niej wykonana, czy nie. W ten sposób funkcja zostanie wykonana co najwyżej raz dla każdej maski, co znacznie przyspieszy algorytm.

Widzimy, że złożoność zmodyfikowanego rozwiązania to $O (2^{n} \cdot n^{2})$ , gdyż dla każdej z $2^{n}$ masek wykonujemy naszą funkcję dokładnie raz. Każde takie wykonanie wymaga $O (n^{2})$ operacji, gdyż musimy rozważyć wszystkie pozostałe pary robotów. Takie rozwiązanie pozwalało zaliczyć podzadanie, w którym $n \leq 20$ .

Rozwiązanie dla $n \leq 1000$

Aby przyspieszyć nasze rozwiązanie, nie możemy dalej symulować wszystkich możliwych gier. Skorzystamy z następującej interpretacji geometrycznej: $i$ -tego robota możemy potraktować jako punkt o współrzędnych $z_{i}, s_{i}$ na płaszczyźnie. Standardowo przyjmiemy, że punkt $(0, 0)$ znajduje się w lewym dolnym rogu płaszczyzny, a osie rosną w prawo i w górę. Wtedy pojedynek robotów o numerach $i$ i $j$ kończy się wyeliminowaniem ich obu, wtedy gdy prosta łącząca odpowiadające im punkty ma ujemny współczynnik kierunkowy. W przeciwnym przypadku jeden z robotów (ten bliżej punktu $(0, 0)$ ) zostaje wyeliminowany, a drugi pozostaje w turnieju. Innymi słowy, roboty wyeliminują się wzajemnie, gdy jeden z nich znajduje się na lewo i do góry względem drugiego. W przeciwnym przypadku, czyli gdy jeden robot znajduje się na lewo i w dół względem drugiego, to ten robot zostanie wyeliminowany, a drugi pozostanie w turnieju. Obie sytuacje są przedstawione na rysunkach poniżej.

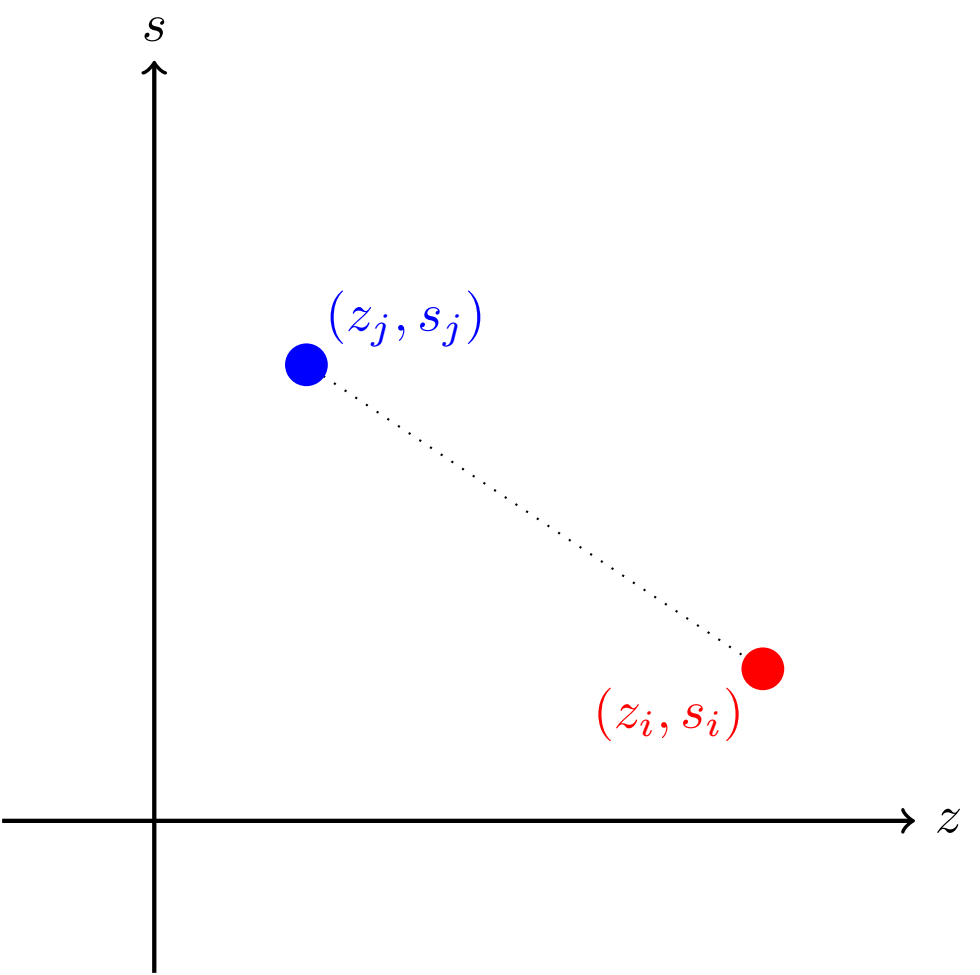
Przykład 2: jeden robot znajduje się na lewo i w dół względem drugiego.

Przykład 1. Robot o numerze $j$ znajduje się w górę i na lewo względem robota o numerze $i$ . W tej sytuacji oba roboty zostaną wyeliminowane w wyniku pojedynku.

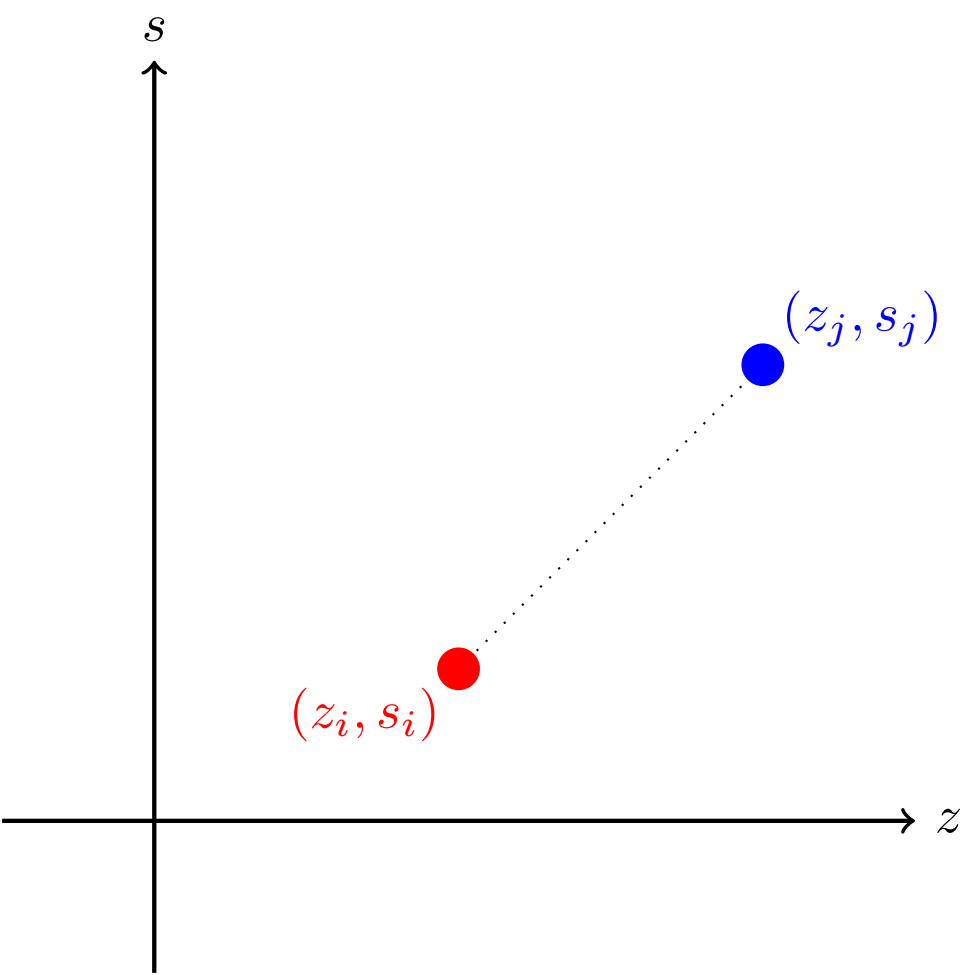
Przykład 1: jeden robot znajduje się na lewo i do góry względem drugiego.

Przykład 2. Robot o numerze $i$ znajduje się w dół i na lewo względem robota o numerze $j$ . W tej sytuacji w wyniku pojedynku robot $i$ zostanie wyeliminowany, a robot $j$ nie.

Patrząc na zadanie w ten sposób, możemy wprowadzić pojęcie zbioru majoryzującego robotów. Powiemy, że zbiór majoryzujący robotów to taki zbiór robotów, który spełnia następujące warunki:

każda para robotów z tego zbioru eliminuje się wzajemnie przy pojedynku,
dla każdego robota spoza zbioru majoryzującego istnieje robot ze zbioru majoryzującego, który go wyeliminuje i przy tym sam nie zostanie wyeliminowany.

Aby lepiej lepiej zilustrować tę definicję, rozważmy przykładową sytuację, w której mamy 7 robotów o wartościach $(z_{i}, s_{i})$ równych kolejno $(1, 5)$ , $(5, 4)$ , $(2, 7)$ , $(3, 6)$ , $(6, 1)$ , $(4, 2)$ , $(7, 3)$ . Jako ćwiczenie dla Czytelnika pozostawmy sprawdzenie, że roboty o numerach 3,4,2,7 tworzą zbiór majoryzujący. Aby przejść do dalszych analiz, spójrzmy najpierw na ten przykład na diagramie stworzonym analogicznie do diagramów wyżej.

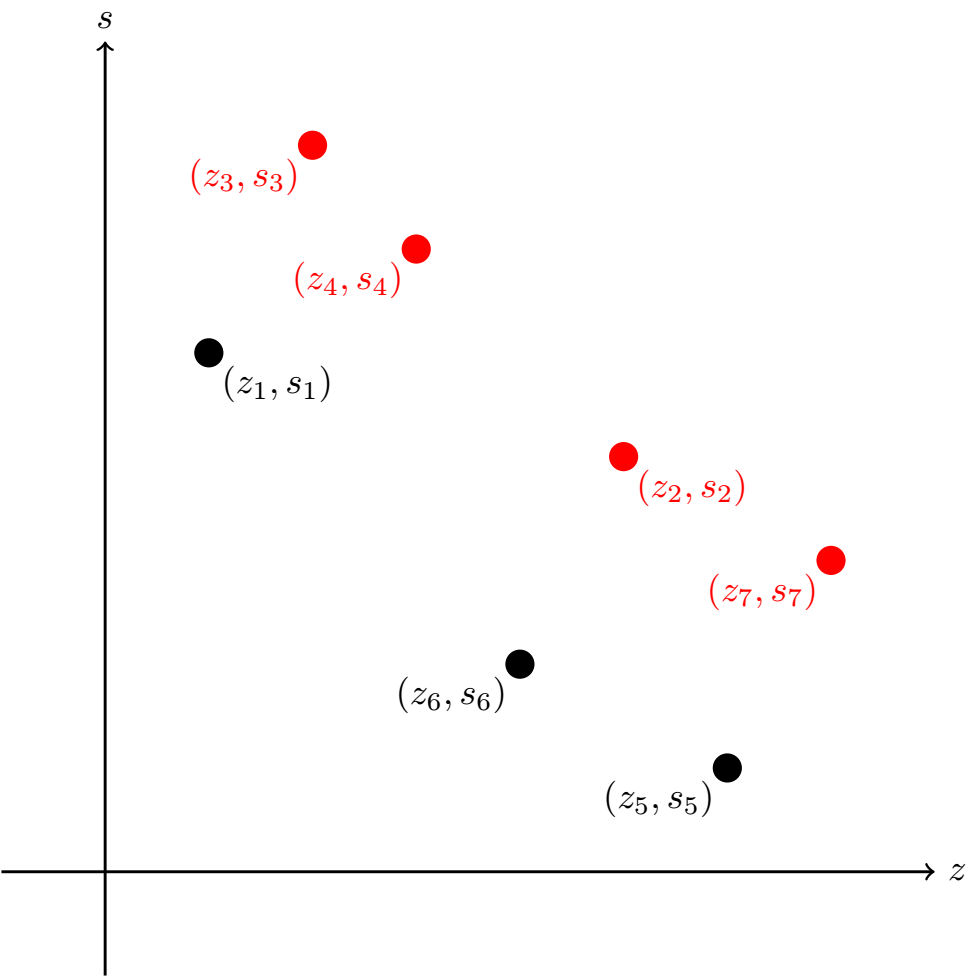
Przykład 3: sytuacja ilustrująca zbiór majoryzujący.

Przykład 3: Sytuacja ilustrująca zbiór majoryzujący. Roboty należące do tego zbioru zostały zaznaczone kolorem czerwonym.

Analiza powyższego diagramu (oraz być może kilku innych dla innych sytuacji) pozwala nam w intuicyjny sposób sformułować pomocniczy lemat.

Lemat

Załóżmy, że roboty są posortowane względem wartości ich siły, czyli $s_{1} = 1, s_{2} = 2, \dots, s_{n} = n$ . Wówczas zbiór majoryzujący to zbiór wszystkich robotów o numerach $i$ takich, że dla każdego robota o numerze $j > i$ zachodzi $z_{j} < z_{i}$ .

Dowód lematu

Załóżmy, że roboty są posortowane względem wartości ich siły, czyli $s_{1} = 1, s_{2} = 2, \dots, s_{n} = n$ . Niech $A \subseteq {1, 2, \dots, n}$ będzie zbiorem numerów robotów, które spełniają warunek z treści lematu. Pokażemy, że $A$ jest zbiorem majoryzującym.

Najpierw weźmy dwa różne numery robotów $k_{1}, k_{2}$ ze zbioru $A$ . Załóżmy bez straty ogólności, że $k_{1} < k_{2}$ . Musimy pokazać, że roboty o tych numerach wzajemnie eliminują się w wyniku walki. Z założenia o tym, że roboty są posortowane według siły mamy $s_{k_{1}} < s_{k_{2}}$ . Ponadto z definicji zbioru $A$ mamy, że dla dowolnego robota o numerze $j > k_{1}$ mamy $z_{j} < z_{k_{1}}$ . W szczególności, biorąc $j = k_{2}$ , mamy $z_{k_{2}} < z_{k_{1}}$ . Widzimy więc, że robot o numerze $k_{1}$ jest zwinniejszy od tego o numerze $k_{2}$ , ale nie jest silniejszy. Wnioskujemy, że w wyniku walki roboty o numerach $k_{1}$ i $k_{2}$ eliminują się wzajemnie.

Teraz weźmy numer robota $i$ taki, że $i$ nie należy do zbioru $A$ . Musimy pokazać, że w zbiorze $A$ istnieje pewien numer robota taki, że robot o tym numerze eliminuje robota o numerze $i$ w wyniku pojedynku i sam nie zostaje wyeliminowany. Skoro $i$ nie należy do $A$ , to musi istnieć pewien robot o numerze $j > i$ taki, że $z_{j} > z_{i}$ . Weźmy największe $j$ spełniające tę własność. Z założenia o posortowaniu robotów po sile mamy $s_{j} > s_{i}$ , a zatem robot o numerze $j$ jest zarówno silniejszy, jak i zwinniejszy od tego o numerze $i$ . Widzimy więc, że w wyniku pojedynku robot o numerze $i$ zostaje wyeliminowany, a ten o numerze $j$ nie. Pozostało nam jedynie pokazać, że $j$ należy do zbioru $A$ . Udowodnimy to przez sprzeczność. Przypuśćmy, że tak nie jest. Wówczas istnieje robot o numerze $k > j$ taki, że $z_{k} > z_{j}$ . Wtedy $z_{k} > z_{j} > z_{i}$ , a zatem $j$ nie jest największa liczbą o tej własności, że $z_{j} > z_{i}$ . Otrzymana sprzeczność pokazuje, że $j$ należy do zbioru $A$ , i kończy dowód lematu.

Co daje nam lemat?

Z lematu otrzymujemy prosty algorytm pozwalający nam znaleźć zbiór majoryzujący. Najpierw sortujemy roboty po ich sile, a następnie przeglądamy je w kolejności sił od największej do najmniejszej. Jeżeli przeglądany obecnie robot jest zwinniejszy od wszystkich przeglądanych dotychczas, to wrzucamy go do zbioru majoryzującego. Największą ze zwinności przeglądanych robotów możemy utrzymywać podczas ich przeglądania i aktualizować, biorąc maksimum przy każdym przeglądanym robocie. Taki algorytm można zaimplementować w złożoności $O (n)$ , o ile tylko jako algorytm sortowania wybierzemy sortowanie kubełkowe.

Dalej zauważmy, że znalezienie zbioru majoryzującego pozwala nam wyznaczyć odpowiedź. Po pierwsze, jeśli rozmiar zbioru majoryzującego jest parzysty, wówczas możemy wyeliminować z turnieju wszystkie roboty spoza tego zbioru w taki sposób, aby żaden robot ze zbioru majoryzującego nie został wyeliminowany. Wynika to wprost z definicji zbioru majoryzującego - dla każdego robota spoza tego zbioru istnieje robot z tego zbioru, który go eliminuje i sam nie zostaje wyeliminowany. Następnie pozostałe roboty ze zbioru majoryzującego dowolnie łączymy w pary i w takich parach przeprowadzamy walki. Założyliśmy, że dowolne dwa roboty ze zbioru majoryzującego eliminują się, a więc po takiej operacji nie pozostanie żaden robot. Otrzymujemy więc, że gdy rozmiar zbioru majoryzującego jest parzysty, odpowiedzią zawsze będzie "TAK".

Pozostało nam rozważyć przypadek, w którym rozmiar zbioru majoryzującego jest nieparzysty. W tym momencie, analizując przypadek wyżej, intuicja mogłaby podpowiadać, że w tym wypadku odpowiedzią zawsze będzie "NIE". Jednak nie zawsze jest to prawda. Zauważmy, że może istnieć pewien robot spoza zbioru majoryzującego (którego numer oznaczmy przez $i$ ) taki, że w wyniku pojedynku eliminuje on pewnego robota (którego numer oznaczymy przez $j$ ) ze zbioru majoryzującego. Wówczas możemy postąpić następująco: Najpierw za pomocą robotów ze zbioru majoryzującego usuwamy wszystkie roboty spoza tego zbioru, pomijając $i$ . Robimy to analogicznie do przypadku, w którym rozmiar zbioru majoryzującego jest parzysty. Następnie roboty $i$ oraz $j$ odbywają walkę, w wyniku której eliminują się nawzajem. Wówczas pozostają nam wszystkie roboty ze zbioru majoryzującego poza robotem o numerze $j$ . Jest ich parzyście wiele, a zatem możemy je połączyć tak w pary, aby wszystkie się wyeliminowały.

Pozostało nam tylko pokazać, że roboty o numerach $i$ oraz $j$ rzeczywiście wzajemnie się wyeliminują. Założyliśmy, że $i$ wyeliminuje $j$ w wyniku pojedynku. Dlaczego $i$ także zostanie wyeliminowane? Zauważmy, że gdyby robot $i$ był zarówno silniejszy jak i zwinniejszy od robota $j$ , to wówczas, na mocy lematu, $j$ nie należałby do zbioru majoryzującego. Stąd w wyniku walki robotów o numerach $i$ oraz $j$ oba zostaną wyeliminowane.

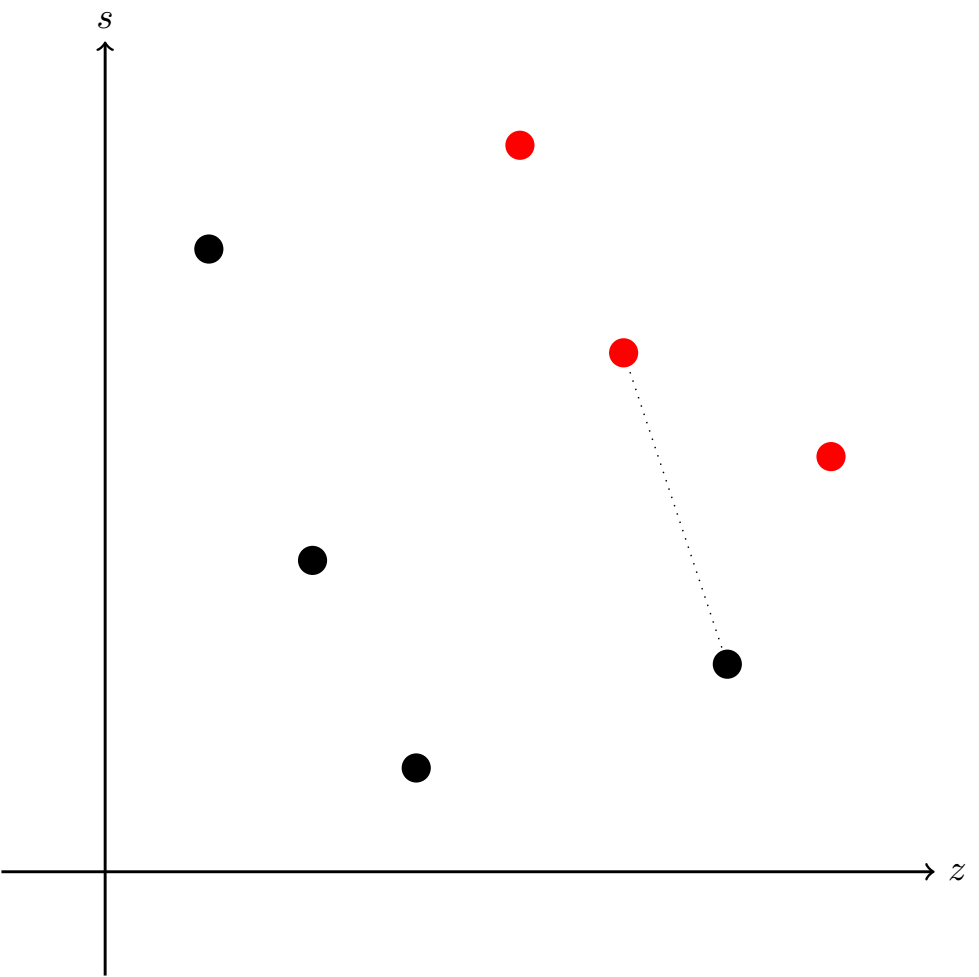
Przykład 4: Sytuacja ilustrująca robota spoza zbioru majoryzującego,
który eliminuje robota z tego zbioru.

Przykład 4: sytuacja ilustrująca robota spoza zbioru majoryzującego, który eliminuje robota z tego zbioru. Odpowiednia para robotów została połączona linią przerywaną.

Widzimy więc, że jeśli istnieje robot o numerze $i$ spełniający własności jak wyżej, to odpowiedzią w zadaniu jest "TAK".

Dalej zauważmy, że jeśli nie istnieje robot spoza zbioru majoryzującego, który byłby w stanie wyeliminować pewnego robota ze zbioru majoryzującego, to wówczas jedynym sposobem eliminowania robotów ze zbioru majoryzującego jest walka między dwoma robotami z tego zbioru. Z definicji tego zbioru wiemy, że taka walka kończy się wyeliminowaniem obu robotów. Skoro robotów w tym zbiorze jest nieparzyście wiele, a ich liczba może maleć tylko o dwa, to zawsze pozostanie nam przynajmniej jeden, a więc nigdy nie uda nam się wyeliminować wszystkich. Otrzymujemy, że wówczas odpowiedzią jest "NIE".

Algorytm

Na podstawie tych rozważań możemy opisać prosty algorytm rozwiązujący nasze zadanie. Najpierw wyznaczamy zbiór majoryzujący robotów w czasie $O (n)$ zgodnie z wnioskiem z lematu. Gdy rozmiar zbioru majoryzującego jest parzysty, odpowiadamy "TAK" i kończymy. W przeciwnym przypadku przeglądamy wszystkie roboty spoza zbioru majoryzującego po kolei i dla każdego z nich sprawdzamy, czy eliminuje on pewnego robota ze zbioru majoryzującego. Jeśli znajdziemy odpowiednią parę, odpowiadamy "TAK". W przeciwnym przypadku odpowiadamy "NIE". Czas działania tego algorytmu to $O (n^{2})$ ze względu na pesymistycznie kwadratowe przeglądanie wszystkich par robotów spoza i ze zbioru majoryzującego. Takie rozwiązanie pozwala zaliczyć podzadanie numer 3.

Pełne rozwiązanie

Od pełnego rozwiązania dzieli nas już tylko jedno spostrzeżenie. Zauważmy, że jako kandydatów spoza zbioru majoryzującego wystarczy rozważyć co najwyżej dwa roboty - te o maksymalnej wartości siły lub zwinności.

Dlaczego to prawda? Załóżmy, że $(z_{i}, s_{i})$ to robot o największej zwinności spośród robotów spoza zbioru majoryzującego, a $(z_{j}, s_{j})$ jest robotem o największej sile spoza tego zbioru. Być może zachodzi $i = j$ . Jeśli roboty o numerach $i$ oraz $j$ nie są w stanie wyeliminować żadnego robota ze zbioru majoryzującego, to oznacza to, że dla dowolnego robota o numerze $k$ ze zbioru majoryzującego mamy $z_{k} > z_{i}$ oraz $s_{k} > s_{j}$ . Skoro założyliśmy, że $z_{i}$ to największa zwinność robotów spoza zbioru majoryzującego, a $s_{j}$ to największa siła robotów ze zbioru majoryzującego, to dla dowolnego numeru $l$ robota spoza zbioru majoryzującego mamy $z_{k} > z_{i} \geq z_{l}$ oraz $s_{k} > s_{j} \geq s_{l}$ , a zatem robot o numerze $l$ nie może wyeliminować robota o numerze $k$ . Z dowolności $l$ i $k$ widzimy, że żaden robot spoza zbioru majoryzującego nie jest w stanie wyeliminować żadnego robota z tego zbioru.

Udało nam się więc pokazać, że jeśli roboty o numerach $i$ oraz $j$ nie pokonują żadnego robota ze zbioru majoryzjącego, to żaden inny robot spoza zbioru majoryzującego nie jest w stanie pokonać żadnego robota z tego zbioru. Stąd wnioskujemy, że istotnie wystarczy sprawdzić roboty o numerach $i$ oraz $j$ .

Dzięki tej obserwacji, możemy sformułować następujący algorytm: Najpierw sortujemy roboty względem wartości ich sił, następnie wyznaczamy zbiór majoryzujący i dalej, jeśli rozmiar tego zbioru jest parzysty, odpowiadamy "TAK" i kończymy. W przeciwnym przypadku szukamy robotów o maksymalnych wartościach siły i zwinności pośród robotów spoza tego zbioru. Jeśli takie nie istnieją (zbiór majoryzujący zawiera wszystkie roboty), to odpowiadamy "NIE" i kończymy. W przeciwnym przypadku sprawdzamy czy znalezione przez nas roboty (co najwyżej dwa) są w stanie wyeliminować jakiegoś robota ze zbioru majoryzującego. Jeśli okaże się, że tak, to odpowiadamy "TAK". W przeciwnym przypadku odpowiadamy "NIE". Takie rozwiązanie można zaimplementować w złożoności czasowej $O (n)$ , co pozwala rozwiązać zadanie w pełni.

Rozwiązanie alternatywne

Po dokładniejszej analizie okazuje się, że prawdziwa jest następująca obserwacja. Załóżmy, że roboty są posortowane po sile, czyli $s_{1} = 1, s_{2} = 2, \dots, s_{n} = n$ . Niech $k$ będzie największą taką liczbą, że ciąg liczb $z_{i}$ ma sufiks postaci $n, n - 1, \dots, n - k + 1$ (może zajść $k = 0$ , gdy taki sufiks nie istnieje). Wówczas odpowiedzią jest "NIE" wtedy i tylko wtedy, gdy $k$ jest nieparzyste. Nietrudny dowód tej obserwacji pozostawimy Czytelnikowi.

Znalezenie takiego $k$ jest proste. Zauważmy, że jeśli $k > 0$ , to taki sufiks musi zaczynać się na pozycji $i$ , dla której $z_{i} = n$ , a więc, o ile $k > 0$ , to jest ono wyznaczone jednoznacznie. Możemy więc obliczyć Przykład 4: sytuacja ilustrująca robota spoza zbioru majoryzującego,
który eliminuje robota z tego zbioru.

Przykład 5: Sytuacja, w której nie istnieje robot spoza zbioru majoryzującego, który eliminowałby pewnego robota z tego zbioru. Zgodnie z obserwacją wyżej, wówczas istnieje sufiks liczb $z_{i}$ postaci $n, n - 1, \dots, n - k + 1$ długości nieparzystej, w tym przypadku dla $k = 3$ .

Takie rozwiązanie oczywiście nie jest szybsze od rozwiązania opisanego powyżej - oba działają w złożoności $O (n)$ . Powyższa obserwacja pozwala natomiast na krótszą i bardziej elegancką implementację.

Opis przygotowano w ramach projektu "Mistrzostwa w Algorytmice i Programowaniu - Uczniowie" - zadania finansowanego ze środków Ministerstwa Cyfryzacji.