Omówienie zadania Drzewo genealogiczne (II etap XXXII OI)

Treść zadania

W zadaniu mamy daną liczbę całkowitą \(n\) oraz dwa napisy długości \(2^n\), przy czym pierwszy oznacza nazwisko Bajtazara, a drugi litery będące jednoliterowymi nazwiskami przodków Bajtazara w odległości \(n\) od niego w drzewie genealogicznym (tych przodków jest \(2^n\)).

Na podstawie przodków możemy stworzyć nazwisko. Dzieje się to w następujący sposób: przodkowie są naturalnie połączeni w pary - pierwszy z drugim, trzeci z czwartym itd. Z każdej z tych par powstaje jeden potomek, którego nazwisko jest konkatenacją (połączeniem napisów) nazwisk jego rodziców. W ten sposób otrzymujemy \(2^{n-1}\) potomków o nazwiskach będących napisami długości \(2\). Ten proces powtarzamy tak długo, aż pozostanie nam jedna osoba z nazwiskiem długości \(2^n\) i to nazwisko jest wynikiem.

Przy łączeniu nazwisk potomków mamy jednak dowolność. Nazwiska mogą być łączone arbitralnie (najpierw nazwisko pierwszego, a potem drugiego lub na odwrót), co sprawia, że w wyniku powyższego procesu możemy otrzymać bardzo wiele różnych nazwisk. Naszym celem jest sprawdzenie, czy nazwisko Bajtazara jest jednym z nich. Dodatkowo musimy obsługiwać aktualizacje pojedynczych liter napisów danych na wejściu i po każdej takiej aktualizacji ponownie stwierdzić, czy nazwisko Bajtazara jest możliwe do otrzymania.

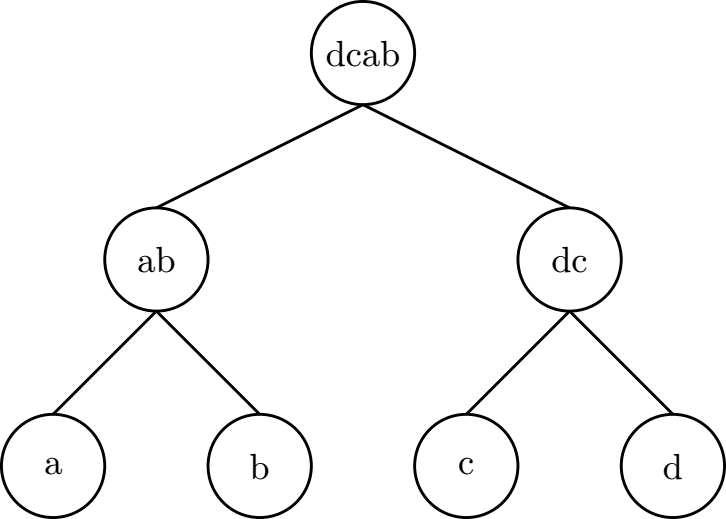
Poniższy rysunek ilustruje możliwe do uzyskania drzewo genealogiczne, gdzie nazwiska \(n\)-tych przodków są opisane napisem abcd. Zauważmy, że możliwych do uzyskania nazwisk jest wiele więcej.

Podzadanie 1 \(n\leq 4, q=0\)

Przy ograniczeniach tego podzadania możemy wygenerować wszystkie możliwe do otrzymania nazwiska i sprawdzić, czy nazwisko Bajtazara jest jednym z nich. Zauważmy, że różnych sposobów na wygenerowanie nazwiska jest dokładnie \(2^{2^{n}-1}\) (przy czym może się zdarzyć, że przy dwóch różnych sposobach wygenerujemy to samo nazwisko), ponieważ mamy dokładnie \(2^{n}-1\) wierzchołków z drzewa genealogicznego, w których podejmujemy decyzję co do kolejności złączania nazwisk rodziców. W ten sposób otrzymujemy algorytm o złożoności \(O(2^{2^{n}}\cdot 2^n)\), gdyż dla każdego wygenerowanego nazwiska w złożoności \(O(2^n)\) sprawdzamy, czy jest nazwiskiem Bajtazara.

Podzadanie 2 \(n\leq 10,q=0\)

Zobaczmy, że jeśli nazwisko Bajtazara może zostać utworzone z nazwisk jego przodków, to pierwsza połowa jego nazwiska musi być możliwa do otrzymania jako nazwisko jednego z rodziców Bajtazara, a druga jako nazwisko drugiego rodzica. Problem polega na tym, że nie wiemy, który z rodziców Bajtazara jest tym pierwszym, więc musimy sprawdzić oba przypadki.

Możemy więc skorzystać z algorytmu rekurencyjnego. Jeśli chcemy porównać, czy jakiś napis może być nazwiskiem pewnego z potomków Bajtazara, to mamy dwie możliwości:

1. Napis ten jest jednoliterowy (i wówczas potomek także ma jednoliterowe nazwisko) - w tym przypadku wystarczy porównać jedyne litery nazwiska i napisu.
2. Napis ten jest dłuższy niż jedna litera (i wówczas potomek ma dwoje rodziców) - wówczas rekurencyjnie sprawdzamy, czy pierwsza połowa napisu jest nazwiskiem pierwszego lub drugiego rodzica (dwa wywołania rekurencyjne) oraz czy druga połowa napisu jest nazwiskiem pierwszego lub drugiego rodzica (znowu dwa wywołania rekurencyjne). Jeśli pierwsza połowa napisu może być nazwiskiem jednego z rodziców, a druga nazwiskiem tego drugiego rodzica, to odpowiedź jest pozytywna. W przeciwnym przypadku jest ona negatywna.

Zobaczmy, że w ten sposób otrzymujemy algorytm, który na każdym poziomie rekurencji wykonuje 4 wywołania rekurencyjne, a poza tym wykonuje stałą liczbę operacji. Głębokość rekurencji wynosi \(O(n)\), gdyż po \(n\) krokach dochodzimy do jednoliterowego napisu. W związku z tym złożoność tego algorytmu możemy oszacować jako \(O(4^n)\).

Podzadanie 3 \(q=0\)

Uwaga: ze względu na to, że w tym zadaniu mamy do czynienia z drzewami genealogicznymi, w dalszej części omówienia pojęcia rodzic i dziecko będą o oznaczały co innego niż to, do czego może być przyzwyczajony Czytelnik zaznajomiony z pojęciem drzewa w informatyce. Dokładniej, w tym zadaniu znaczenia tych słów zostały ze sobą zamienione względem standardowo przyjętych konwencji.

Będziemy rozważać także nazwisko Bajtazara jako drzewo genealogiczne. Ponadto załóżmy, że przy łączeniu nazwisk rodziców zawsze jako pierwszego wybieramy lewego rodzica. Oznaczmy drzewo składające się z nazwisk przodków Bajtazara przez \(A\), a drzewo zbudowane na nazwisku Bajtazara przez \(B\). Wówczas interesuje nas, czy za pomocą pewnej liczby operacji zamiany kolejności rodziców w wierzchołkach drzewa \(A\) możemy sprawić, aby było ono takie samo jak drzewo \(B\). Jest tak dlatego, że, zgodnie w przyjętą tu konwencją, zamiana kolejności rodziców w \(A\) odpowiada zamianie kolejności złączania nazwisk tych rodziców. Naturalnie przyjmujemy, że drzewa są takie same, gdy mają takie same napisy w odpowiadających sobie wierzchołkach.

Zauważmy, że operacje, które wykonujemy, są odwracalne i same są swoimi odwrotnościami. Jeśli zamienimy rodziców pewnego wierzchołka w drzewie, a następnie zamienimy ich jeszcze raz, to drzewo będzie takie same jak przed modyfikacjami.

Możemy także zaobserwować, że równoważne naszemu pytaniu jest pytanie, czy za pomocą operacji zamiany kolejności rodziców w drzewie \(B\), możemy sprawić, aby \(B\) było takie same jak \(A\). Dlaczego? Załóżmy, że za pomocą pewnej sekwencji zamian rodziców w drzewie \(A\) możemy przetransformować je w drzewo \(B\). Nietrudno sprawdzić, że wówczas, stosując tę sekwencję w odwrotnej kolejności do wierzchołków drzewa \(B\), możemy przetransformować je w drzewo \(A\).

Na podstawie tych wniosków możemy skorzystać z pomysłu, który często pojawia się w zadaniach, gdzie należy sprawdzić, czy dwa obiekty są takie same z dokładnością do pewnych operacji: postaramy się dla obu obiektów wyznaczyć ich kanoniczne formy, a następnie sprawdzić, czy te formy są takie same.

Jako kanoniczną formę danego drzewa \(X\) przyjmiemy drzewo \(Y\) powstałe z pewnej liczby operacji zamiany kolejności rodziców w wierzchołkach drzewa \(X\) takie, że napis w korzeniu (najwyższym wierzchołku) drzewa \(Y\) jest najmniejszy leksykograficznie spośród wszystkich napisów możliwych do otrzymania w korzeniu dzięki takim operacjom.

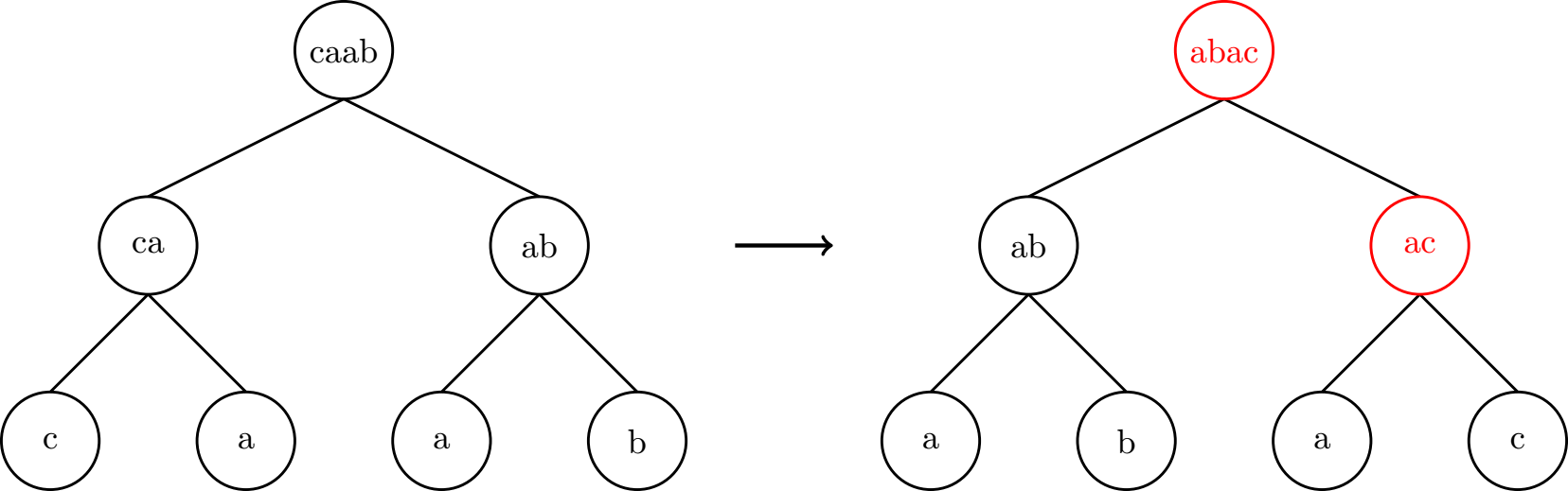
Pozostało tylko uzasadnić, że możemy otrzymać jedno drzewo z drugiego wtedy i tylko wtedy, gdy ich kanoniczne formy są takie same.

Załóżmy najpierw, że kanoniczne formy drzew \(A\) i \(B\) są takie same. Wówczas dla obu drzew istnieją sekwencje operacji, które doprowadzają je do tej kanonicznej formy. Możemy więc sprowadzić drzewo \(A\) do kanonicznej formy, a następnie wykonać na nim operacje, które przekształcą tę kanoniczną formę w drzewo \(B\), wykonując operacje odwrotne do tych, które przekształciłyby drzewo \(B\) do kanonicznej formy.

Następnie załóżmy, że drzewo \(A\) można przekształcić w drzewo \(B\). Wówczas każdy napis, który możemy otrzymać w korzeniu drzewa \(B\), możemy otrzymać w korzeniu drzewa \(A\). Skoro nasze operacje są odwracalne, to wiemy także, że drzewo \(B\) można przekształcić w drzewo \(A\). Stąd wszystkie napisy, które możemy otrzymać w korzeniu drzewa \(A\), możemy otrzymać w korzeniu drzewa \(B\). Uzyskujemy więc, że napisy, które możemy otrzymać w korzeniu drzewa \(A\) to dokładnie te same, które możemy otrzymać w korzeniu drzewa \(B\). W szczególności najmniejszy leksykograficznie napis, który możemy otrzymać w korzeniach obu drzew jest taki sam.

Pozostało tylko pytanie: jak wyznaczyć kanoniczną formę drzewa? Możemy to zrobić, przechodząc drzewo w kierunku od liści (wierzchołków na ostatnim poziomie drzewa) do korzenia. Dla każdego wierzchołka wyznaczmy najmniejszy leksykograficznie napis, który możemy otrzymać w tym wierzchołku.

Dla liścia jest to oczywiście jednoliterowy napis zapisany w tym liściu. Dla wierzchołka wewnętrznego wyznaczmy najmniejszy leksykograficznie napis, który możemy otrzymać w tym wierzchołku na podstawie najmniejszych leksykograficznie napisów, które możemy otrzymać w jego rodzicach. Znając te napisy, porównujemy je ze sobą i jako pierwszy wybieramy ten, który jest mniejszy, a następnie do niego doklejamy drugi napis.

W ten sposób nasz algorytm wyznaczania kanonicznej formy drzewa działa w złożoności \(O(n\cdot 2^n)\), gdyż na każdym poziomie drzewa wykonujemy \(O(2^n)\) operacji. Zainteresowany Czytelnik może zauważyć, że analiza złożoności tego algorytmu jest bardzo podobna do analizy złożoności algorytmu sortowania przez scalanie (merge sort).

Podzadanie 4 \(n\leq 18,q\leq 200'000\)

W tym podzadaniu skorzystamy z pomysłu z poprzedniego podzadania, jednak zamiast jawnie wyznaczać najmniejsze leksykograficznie napisy możliwe do otrzymania w wierzchołkach drzewa, będziemy przechowywać ich wielomianowe hasze. O wielomianowym haszowaniu napisów można przeczytać więcej w omówieniu zadania Okropny wiersz z XIX OI.

Będziemy wyznaczać hasze wierzchołków drzewa począwszy od liści w górę. Dla liści jest to oczywiście hasz jednoliterowych napisów. Dalej załóżmy, że mamy pewien wierzchołek niebędący liściem i znamy hasze jego rodziców. Załóżmy, że hasz rodzica, którego najmniejszy leksykograficznie napis jest mniejszy, to \(h_1\), a hasz drugiego rodzica to \(h_2\). Załóżmy ponadto, że obaj rodzice mają w swoich poddrzewach \(2^k\) liści. Wówczas hasz wierzchołka to \[ h = \left(h_1\cdot p^{2^k} + h_2\right) \bmod m, \] gdzie \(p\) to podstawa haszowania, a \(m\) to liczba będąca wartością modulo.

Pozostało jednak odpowiedzieć na pytanie, w jaki sposób wyznaczyć, który z rodziców odpowiada mniejszemu leksykograficznie napisowi. Skoro nie trzymamy już dłużej napisów w wierzchołkach, to musimy poradzić sobie jakoś inaczej.

Skorzystamy z techniki, która często idzie w parze z haszowaniem napisów. Aby porównać dwa napisy, możemy za pomocą wyszukiwania binarnego wyznaczyć pierwszą pozycję, na której są one różne. Wówczas porównanie napisów sprowadza się do porównania ich znaków na tej pozycji.

Zauważmy, że struktura naszego drzewa w naturalny sposób ułatwia nam wyszukiwanie binarne. Załóżmy, że chcemy porównać napisy odpowiadające dwóm wierzchołkom \(v_1\) i \(v_2\) znajdującym się na tej samej głębokości w drzewie. Jeśli oba wierzchołki to liście, to wystarczy porównać ich jedyne litery. W przeciwnym wypadku hasz pierwszego wierzchołka jest postaci \[ h_1 = \left(h_{11}\cdot p^{2^{k}} + h_{12}\right) \bmod m, \] a hasz drugiego wierzchołka to \[ h_2 = \left(h_{21}\cdot p^{2^{k}} + h_{22}\right) \bmod m, \] gdzie \(h_{11}\) i \(h_{12}\) to hasze rodziców \(v_1\), przy czym \(h_{11}\) odpowiada rodzicowi o mniejszym leksykograficznie napisie, i analogicznie dla \(h_{21}\) i \(h_{22}\). Wówczas, jeśli \(h_{11}=h_{21}\), to z bardzo dużym prawdopodobieństwem pierwsza połowa napisów w wierzchołkach \(v_1\) i \(v_2\) jest taka sama. W takim wypadku możemy porównać drugie połowy napisów w tych wierzchołkach przez rekurencyjne wywołanie tej procedury na rodzicach, którym odpowiadają hasze \(h_{12}\) i \(h_{22}\). Jeśli \(h_{11}\not=h_{21}\), to wiemy, że pierwsze połowy napisów w wierzchołkach \(v_1\) i \(v_2\) są różne, więc można rekurencyjnie wywołać tę procedurę na rodzicach, którym odpowiadają hasze \(h_{11}\) i \(h_{21}\).

W ten sposób po co najwyżej \(n\) krokach dojdziemy do liści i wówczas porównanie napisów sprowadzi się do przypadku bazowego - porównania pojedynczych liter. Aby być w stanie wydajnie zaimplementować tę procedurę, musimy dla każdego wierzchołka pamiętać (na przykład w dodatkowej tablicy), który z jego rodziców odpowiada mniejszemu leksykograficznie napisowi.

W ten sposób, aby porównać, czy jedno drzewo może zostać przetransformowane w drugie, porównujemy wartości haszy w ich korzeniach. Wówczas z dużym prawdopodobieństwem udzielimy poprawnej odpowiedzi.

Ponieważ w drzewie mamy \(2^n-1\) wierzchołków niebędących liśćmi, a dla każdego z nich wykonujemy \(O(n)\) operacji, aby wyznaczyć kolejność synów, to złożoność wyznaczania wszystkich haszy wierzchołków drzewa wynosi \(O(n\cdot 2^n)\). Zauważmy dalej, że przy aktualizacji litery w liściu musimy zaktualizować hasze wszystkich wierzchołków na ścieżce od tego liścia do korzenia. Tych wierzchołków jest dokładnie \(n+1\), a dla każdego z nich wykonujemy \(O(n)\) operacji, zatem złożoność aktualizacji litery w liściu wynosi \(O(n^2)\).

Otrzymujemy zatem rozwiązanie o złożoności \(O(n\cdot 2^n + n^2\cdot q)\).

Podzadanie 5 \(n\leq 20,q\leq 1'000'000\)

W tym podzadaniu ponownie zastosujemy technikę haszowania, jednak porzucimy pomysł z wyznaczaniem haszy najmniejszych leksykograficznie napisów. Zamiast tego dla każdego wierzchołka wyznaczymy pewien hasz w taki sposób, aby wartość tego hasza była niezależna od kolejności rodziców.

Załóżmy, że mamy pewien wierzchołek \(v\). Jeśli \(v\) jest liściem, to hasz wierzchołka to po prostu hasz jednoliterowego napisu w tym liściu. Dalej załóżmy, że \(v\) nie jest liściem i że znamy hasze jego rodziców \(h_1\) oraz \(h_2\), a w poddrzewie każdego z tych rodziców jest \(2^k\) liści. Wówczas hasz wierzchołka \(v\) możemy obliczyć jako \[ h = \left(\min(h_1,h_2)\cdot p^{2^k} + max(h_1,h_2)\right) \bmod m. \] Łatwo przekonać się, że taka funkcja haszująca jest odporna na zamianę kolejności rodziców: wartości \(min(h_1,h_2)\) oraz \(max(h_1,h_2)\) są wyznaczone jednoznacznie, nawet jeśli zamienimy \(h_1\) i \(h_2\) miejscami. Działa to nawet pomimo tego, że hasze są wartościami reszty z dzielenia przez \(m\).

Widzimy więc, że hasz wierzchołka dalej jest haszem pewnego słowa, które można otrzymać w tym wierzchołku poprzez operacje zamiany rodziców na wierzchołkach jego poddrzewa. To słowo nie musi być jednak najmniejsze możliwe w kolejności leksykograficznej. Zauważmy jednak, że tu także wyznaczamy pewien (inny niż leksykograficzny) porządek na słowach, porównując słowa nie ze względu na ich litery, a poprzez porównywanie ich wielomianowych haszy jako liczby.

W związku z tym nasze hasze zachowują pożądane przez nas własności: jeśli hasze w korzeniach obu drzewa są różne, to możemy mieć pewność, że nie da się przetransformować jednego drzewa w drugie. Jeśli natomiast hasze są równe, oznacza to, że z dużym prawdopodobieństwem jest to możliwe.

Dzięki tej zmianie jesteśmy w stanie w czasie stałym wyznaczyć wartość hasza wierzchołka na podstawie wartości haszy jego rodziców. Otrzymujemy więc algorytm o złożoności czasowej \(O(2^n+n\cdot q)\), co pozwala w pełni rozwiązać zadanie.